Question
A thin uniform cylindrical shell, closed at both ends, is partially filled with water. It is floating vertically in water in half-submerged state. If $${\rho _c}$$ is the relative density of the material of the shell with respect to water, then the correct statement is that the shell is-
A.
more than half-filled if $${\rho _c}$$ is less than $$0.5.$$
B.
more than half-filled if $${\rho _c}$$ is more than $$1.0.$$
C.
half-filled if $${\rho _c}$$ is more than $$0.5.$$
D.
less than half-filled if $${\rho _c}$$ is less than $$0.5.$$
Answer :
more than half-filled if $${\rho _c}$$ is less than $$0.5.$$
Solution :
Let $$V$$ be the volume of the material of which the cylinder is made. The cylinder is half immersed in water. Therefore the volume of water displaced because of the material of the cylinder is $$\frac{V}{2}.$$ Let $$h$$ be the total height of the cylinder. As the cylinder is half submerged therefore buoyant force
$$B = \frac{{V{\rho _\omega }g}}{2} + \frac{{hA{\rho _\omega }g}}{2}$$
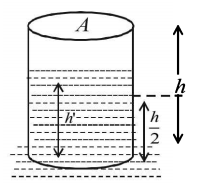
where $$A$$ is the area of cross-section of the cylinder
The weight of the cylinder $$W = V{\rho _c}g$$
The weight of the water inside the cylinder $$ = h'A{\rho _\omega }g$$
For equilibrium,
$$\frac{{V{\rho _\omega }g}}{2} + \frac{{Ah{\rho _\omega }g}}{2} = V{\rho _c}g + = h'A{\rho _\omega }g$$
Here $${\rho _\omega } = 1$$
$$\eqalign{ & \therefore h' = \frac{h}{2} + \frac{V}{{2A}}\,\,\left[ {1 - 2{\rho _c}} \right] \cr & {\text{If }}{\rho _c} < 0.5\,\,{\text{then }}h' > \frac{h}{2} \cr & {\text{and if }}{\rho _c} > 0.5\,\,{\text{then }}h' < \frac{h}{2} \cr & {\text{if }}{\rho _c} = 0,\,\,{\text{ }}h' = \frac{h}{2} \cr} $$
Let $$V$$ be the volume of the material of which the cylinder is made. The cylinder is half immersed in water. Therefore the volume of water displaced because of the material of the cylinder is $$\frac{V}{2}.$$ Let $$h$$ be the total height of the cylinder. As the cylinder is half submerged therefore buoyant force
$$B = \frac{{V{\rho _\omega }g}}{2} + \frac{{hA{\rho _\omega }g}}{2}$$

where $$A$$ is the area of cross-section of the cylinder
The weight of the cylinder $$W = V{\rho _c}g$$
The weight of the water inside the cylinder $$ = h'A{\rho _\omega }g$$
For equilibrium,
$$\frac{{V{\rho _\omega }g}}{2} + \frac{{Ah{\rho _\omega }g}}{2} = V{\rho _c}g + = h'A{\rho _\omega }g$$
Here $${\rho _\omega } = 1$$
$$\eqalign{ & \therefore h' = \frac{h}{2} + \frac{V}{{2A}}\,\,\left[ {1 - 2{\rho _c}} \right] \cr & {\text{If }}{\rho _c} < 0.5\,\,{\text{then }}h' > \frac{h}{2} \cr & {\text{and if }}{\rho _c} > 0.5\,\,{\text{then }}h' < \frac{h}{2} \cr & {\text{if }}{\rho _c} = 0,\,\,{\text{ }}h' = \frac{h}{2} \cr} $$

