Question
A thin uniform annular disc (see figure) of mass $$M$$ has outer radius $$4R$$ and inner radius $$3R.$$ The work required to take a unit mass from point $$P$$ on its axis to infinity is-
A thin uniform annular disc (see figure) of mass $$M$$ has outer radius $$4R$$ and inner radius $$3R.$$ The work required to take a unit mass from point $$P$$ on its axis to infinity is-

A.
$$\frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right)$$
B.
$$ - \frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right)$$
C.
$$\frac{{GM}}{{4R}}$$
D.
$$\frac{{2GM}}{{5R}}\left( {\sqrt 2 - 1} \right)$$
Answer :
$$\frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right)$$
Solution :
Let us consider a circular elemental area of radius $$x$$ and thickness $$dx.$$ The area of the shaded portion \[ = 2\pi xdx.\]
Let $$dm$$ be the mass of the shaded portion.
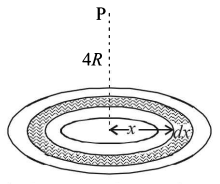
$$\eqalign{ & \therefore \frac{{Mass}}{{Area}} = \frac{M}{{\pi \left( {4{R^2}} \right) - \pi {{\left( {3R} \right)}^2}}} = \frac{{dm}}{{2\pi xdx}} \cr & \therefore dm = \frac{{2M}}{{7{R^2}}}xdx \cr} $$
The gravitational potential of the mass $$dm$$ at $$P$$ is
$$\eqalign{ & dV = \frac{{ - G\,dm}}{{\sqrt {{{\left( {4R} \right)}^2} + {x^2}} }} = - \frac{G}{{\sqrt {16{R^2} + {x^2}} }} \times \frac{{2M}}{{7{R^2}}}xdx \cr & = \frac{{ - 2GM}}{{7{R^2}}}\frac{{xdx}}{{\sqrt {16{R^2} + {x^2}} }}\,.....(1) \cr} $$
suppose $$16{R^2} + {x^2} = {t^2}$$
$$ \Rightarrow 2xdx = 2tdt\,\,\,\,\, \Rightarrow xdx = tdt$$
Also for $$x=3R,\,\,\,\,t=5R$$ and for $$x = 4R,\,\,t = 4\sqrt 2 R$$
On integrating equation (1), taking the above limits, we get:
$$\eqalign{ & V = - \int\limits_{5R}^{4\sqrt 2 R} {\frac{{2GM}}{{7{R^2}}}dt = \frac{{ - 2GM}}{{7{R^2}}}\left[ t \right]_{5R}^{4\sqrt 2 R}} \cr & = \frac{{ - 2GM}}{{7{R^2}}}\left[ {4\sqrt 2 R - 5R} \right] \cr & \Rightarrow V = \frac{{ - 2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right) \cr & {\text{Now }}\frac{{{W_{P\,\infty }}}}{1} = {V_ \propto } - {V_P} = - {V_P}\,\,\,\,\,\,\,\,\left[ {\because {V_ \propto } = 0} \right] \cr & \therefore {W_{P\,\infty }} = \frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right) \cr} $$
Let us consider a circular elemental area of radius $$x$$ and thickness $$dx.$$ The area of the shaded portion \[ = 2\pi xdx.\]
Let $$dm$$ be the mass of the shaded portion.

$$\eqalign{ & \therefore \frac{{Mass}}{{Area}} = \frac{M}{{\pi \left( {4{R^2}} \right) - \pi {{\left( {3R} \right)}^2}}} = \frac{{dm}}{{2\pi xdx}} \cr & \therefore dm = \frac{{2M}}{{7{R^2}}}xdx \cr} $$
The gravitational potential of the mass $$dm$$ at $$P$$ is
$$\eqalign{ & dV = \frac{{ - G\,dm}}{{\sqrt {{{\left( {4R} \right)}^2} + {x^2}} }} = - \frac{G}{{\sqrt {16{R^2} + {x^2}} }} \times \frac{{2M}}{{7{R^2}}}xdx \cr & = \frac{{ - 2GM}}{{7{R^2}}}\frac{{xdx}}{{\sqrt {16{R^2} + {x^2}} }}\,.....(1) \cr} $$
suppose $$16{R^2} + {x^2} = {t^2}$$
$$ \Rightarrow 2xdx = 2tdt\,\,\,\,\, \Rightarrow xdx = tdt$$
Also for $$x=3R,\,\,\,\,t=5R$$ and for $$x = 4R,\,\,t = 4\sqrt 2 R$$
On integrating equation (1), taking the above limits, we get:
$$\eqalign{ & V = - \int\limits_{5R}^{4\sqrt 2 R} {\frac{{2GM}}{{7{R^2}}}dt = \frac{{ - 2GM}}{{7{R^2}}}\left[ t \right]_{5R}^{4\sqrt 2 R}} \cr & = \frac{{ - 2GM}}{{7{R^2}}}\left[ {4\sqrt 2 R - 5R} \right] \cr & \Rightarrow V = \frac{{ - 2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right) \cr & {\text{Now }}\frac{{{W_{P\,\infty }}}}{1} = {V_ \propto } - {V_P} = - {V_P}\,\,\,\,\,\,\,\,\left[ {\because {V_ \propto } = 0} \right] \cr & \therefore {W_{P\,\infty }} = \frac{{2GM}}{{7R}}\left( {4\sqrt 2 - 5} \right) \cr} $$