Question
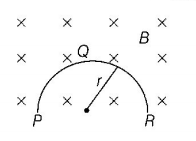
A thin semicircular conducting ring $$\left( {PQR} \right)$$ of radius $$r$$ is falling with its plane vertical in a horizontal magnetic field $$B,$$ as shown in figure. The potential difference developed across the ring when its speed is $$v,$$ is
A thin semicircular conducting ring $$\left( {PQR} \right)$$ of radius $$r$$ is falling with its plane vertical in a horizontal magnetic field $$B,$$ as shown in figure. The potential difference developed across the ring when its speed is $$v,$$ is
A.
zero
B.
$$\frac{{BV\pi {r^2}}}{2}$$ and $$P$$ is at higher potential
C.
$$\pi rBv$$ and $$R$$ is at higher potential
D.
$$2rBv$$ and $$R$$ is at higher potential
Answer :
$$2rBv$$ and $$R$$ is at higher potential
Solution :
An induced emf (BLv) called motional emf is produced by moving a conductor instead of varying the magnetic field.
For emf, $$e = Bv\left( {{L_{{\text{eff}}}}} \right) = Bv \times \left( {2r} \right) = 2Bvr\,\,\left[ {\because {L_{{\text{eff}}}} = {\text{diameter}} = 2r} \right]$$
$$R$$ will be at higher potential, we can find it by using right hand rule. The electrons of wire will move towards end $$P$$ due to electric force and at end $$R$$ the excess positive change will be left.
An induced emf (BLv) called motional emf is produced by moving a conductor instead of varying the magnetic field.
For emf, $$e = Bv\left( {{L_{{\text{eff}}}}} \right) = Bv \times \left( {2r} \right) = 2Bvr\,\,\left[ {\because {L_{{\text{eff}}}} = {\text{diameter}} = 2r} \right]$$
$$R$$ will be at higher potential, we can find it by using right hand rule. The electrons of wire will move towards end $$P$$ due to electric force and at end $$R$$ the excess positive change will be left.
