Question
A thin rod of length $$'L'$$ is lying along the x-axis with its ends at $$x=0$$ and $$x=L.$$ Its linear density (mass/length) varies with $$x$$ as $$k{\left( {\frac{x}{L}} \right)^n},$$ where $$n$$ can be zero or any positive number. If the position $${x_{CM}},$$ of the centre of mass of the rod is plotted against $$'n',$$ which of the following graphs best approximates the dependence of $${x_{CM}},$$ on $$n$$ ?
A.


B.


C.


D.

Answer :


Solution :
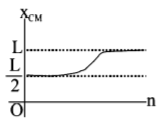
$$ \bullet $$ When $$n=0,\,x=k$$ where $$k$$ is a constant. This means that the linear mass density is constant. In this case the centre of mass will be at the middle of the rod ie at $$\frac{L}{2}.$$
Therefore (C) is ruled out.
$$ \bullet $$ $$n$$ is positive and as its value increases, the rate of increase of linear mass density with increase in $$x$$ increases. This shows that the centre of mass will shift towards that end of the rod where $$n = L$$ as the value of $$n$$ increases.
Therefore graph (B) is ruled out.
$$ \bullet $$ The linear mass density $$\lambda = k{\left( {\frac{x}{L}} \right)^n}{\text{ Here }}\frac{x}{L} \leqslant 1$$
With increase in the value of $$n,$$ the centre of mass shift towards the end $$x = L$$ such that first the shifting is at a higher rate with increase in the value of $$n$$ and then the rate decreases with the value of $$n.$$
These characteristics are represented by graph (A).
$$\eqalign{ & {x_{CM}} = \frac{{\int\limits_0^L {x\,dm} }}{{\int\limits_0^L {dm} }} \cr & = \frac{{\int\limits_0^L {x\,\left( {\lambda \,dx} \right)} }}{{\int\limits_0^L {\lambda \,dx} }} \cr & = \frac{{\int\limits_0^L {k\,{{\left( {\frac{x}{L}} \right)}^n}\,.\,xdx} }}{{\int\limits_0^L {k\,{{\left( {\frac{x}{L}} \right)}^n}\,.\,dx} }} \cr & = \frac{{k\left[ {\frac{{{x^{n + 2}}}}{{\left( {n + 2} \right){L^n}}}} \right]_0^L}}{{\left[ {\frac{{k\,{x^{n + 1}}}}{{\left( {n + 1} \right){L^n}}}} \right]_0^L}} \cr & = \frac{{L\left( {n + 1} \right)}}{{n + 2}} \cr & {\text{For }}n = 0,\,\,\,\,{x_{CM}} = \frac{L}{2};\,\,\,\,n = 1, \cr & {x_{CM}} = \frac{{2L}}{3};\,\,\,\,n = 2,\,\,\,\,{x_{CM}} = \frac{{3L}}{4};\,..... \cr} $$
$$ \bullet $$ When $$n=0,\,x=k$$ where $$k$$ is a constant. This means that the linear mass density is constant. In this case the centre of mass will be at the middle of the rod ie at $$\frac{L}{2}.$$
Therefore (C) is ruled out.
$$ \bullet $$ $$n$$ is positive and as its value increases, the rate of increase of linear mass density with increase in $$x$$ increases. This shows that the centre of mass will shift towards that end of the rod where $$n = L$$ as the value of $$n$$ increases.
Therefore graph (B) is ruled out.
$$ \bullet $$ The linear mass density $$\lambda = k{\left( {\frac{x}{L}} \right)^n}{\text{ Here }}\frac{x}{L} \leqslant 1$$
With increase in the value of $$n,$$ the centre of mass shift towards the end $$x = L$$ such that first the shifting is at a higher rate with increase in the value of $$n$$ and then the rate decreases with the value of $$n.$$
These characteristics are represented by graph (A).
$$\eqalign{ & {x_{CM}} = \frac{{\int\limits_0^L {x\,dm} }}{{\int\limits_0^L {dm} }} \cr & = \frac{{\int\limits_0^L {x\,\left( {\lambda \,dx} \right)} }}{{\int\limits_0^L {\lambda \,dx} }} \cr & = \frac{{\int\limits_0^L {k\,{{\left( {\frac{x}{L}} \right)}^n}\,.\,xdx} }}{{\int\limits_0^L {k\,{{\left( {\frac{x}{L}} \right)}^n}\,.\,dx} }} \cr & = \frac{{k\left[ {\frac{{{x^{n + 2}}}}{{\left( {n + 2} \right){L^n}}}} \right]_0^L}}{{\left[ {\frac{{k\,{x^{n + 1}}}}{{\left( {n + 1} \right){L^n}}}} \right]_0^L}} \cr & = \frac{{L\left( {n + 1} \right)}}{{n + 2}} \cr & {\text{For }}n = 0,\,\,\,\,{x_{CM}} = \frac{L}{2};\,\,\,\,n = 1, \cr & {x_{CM}} = \frac{{2L}}{3};\,\,\,\,n = 2,\,\,\,\,{x_{CM}} = \frac{{3L}}{4};\,..... \cr} $$