Question
A thin flexible wire of length $$L$$ is connected to two adjacent fixed points and carries a current $$I$$ in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength $$B$$ going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is
A thin flexible wire of length $$L$$ is connected to two adjacent fixed points and carries a current $$I$$ in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength $$B$$ going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is

A.
$$IBL$$
B.
$$\frac{{IBL}}{\pi }$$
C.
$$\frac{{IBL}}{{2\pi }}$$
D.
$$\frac{{IBL}}{{4\pi }}$$
Answer :
$$\frac{{IBL}}{{2\pi }}$$
Solution :
Let us consider an elemental length dl subtending an angle $$d\theta $$ at the centre of the circle. Let $${F_B}$$ be the magnetic force acting on this length. Then
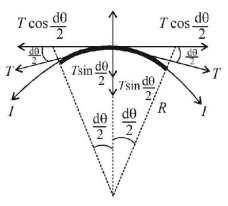
$${F_B} = BI\left( {dl} \right)$$ directed upwards as shown
$$\eqalign{ & = BI\left( {Rd\theta } \right)\,\,\,\,\,\left[ {\because {\text{angle}}\left( {d\theta } \right) = \frac{{arc\left( {dI} \right)}}{{{\text{radius}}R}}} \right] \cr & = BI\left( {\frac{L}{{2\pi }}} \right)d\theta \,\,\,\,\left[ {\because 2\pi R = L \Rightarrow R = \frac{L}{{2\pi }}} \right] \cr} $$
Let $$T$$ be the tension in the wire acting along both ends of the elemental length as shown. On resolving $$T,$$ we find that the components. $$T\cos \left( {\frac{{d\theta }}{2}} \right)$$ cancel out and the components. $$T\sin \left( {\frac{{d\theta }}{2}} \right)$$ add up to balance $${F_B}.$$
At equilibrium $$2T\sin \left( {\frac{{d\theta }}{2}} \right) = BI\frac{L}{{2\pi }}d\theta $$
$$\eqalign{ & \Rightarrow 2T\frac{{d\theta }}{2} = BI\frac{L}{{2\pi }}d\theta \quad \left[ {\because \frac{{d\theta }}{2} = {\text{small}}} \right] \cr & \Rightarrow T = \frac{{BIL}}{{2\pi }} \cr} $$
Let us consider an elemental length dl subtending an angle $$d\theta $$ at the centre of the circle. Let $${F_B}$$ be the magnetic force acting on this length. Then

$${F_B} = BI\left( {dl} \right)$$ directed upwards as shown
$$\eqalign{ & = BI\left( {Rd\theta } \right)\,\,\,\,\,\left[ {\because {\text{angle}}\left( {d\theta } \right) = \frac{{arc\left( {dI} \right)}}{{{\text{radius}}R}}} \right] \cr & = BI\left( {\frac{L}{{2\pi }}} \right)d\theta \,\,\,\,\left[ {\because 2\pi R = L \Rightarrow R = \frac{L}{{2\pi }}} \right] \cr} $$
Let $$T$$ be the tension in the wire acting along both ends of the elemental length as shown. On resolving $$T,$$ we find that the components. $$T\cos \left( {\frac{{d\theta }}{2}} \right)$$ cancel out and the components. $$T\sin \left( {\frac{{d\theta }}{2}} \right)$$ add up to balance $${F_B}.$$
At equilibrium $$2T\sin \left( {\frac{{d\theta }}{2}} \right) = BI\frac{L}{{2\pi }}d\theta $$
$$\eqalign{ & \Rightarrow 2T\frac{{d\theta }}{2} = BI\frac{L}{{2\pi }}d\theta \quad \left[ {\because \frac{{d\theta }}{2} = {\text{small}}} \right] \cr & \Rightarrow T = \frac{{BIL}}{{2\pi }} \cr} $$