Question
A stone tied to the end of a string of $$1\,m$$ long is whirled in a horizontal circle with a constant speed. If the stone makes 22 revolution in 44 seconds, what is the magnitude and direction of acceleration of the stone?
A.
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre.
B.
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius away from the centre.
C.
$${\pi ^2}m{s^{ - 2}}$$ and direction along the tangent to the circle.
D.
$$\frac{{{\pi ^2}}}{4}m{s^{ - 2}}$$ and direction along the radius towards the centre.
Answer :
$${\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre.
Solution :
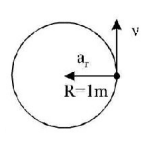
$$\eqalign{ & {a_r} = {\omega ^2}R \cr & {a_r} = {\left( {2\pi 2} \right)^2}R = 4{\pi ^2}{2^2}R \cr & = 4{\pi ^2}{\left( {\frac{{22}}{{44}}} \right)^4}\left( 1 \right)\,\,\left[ {\because v = \frac{{22}}{{44}}} \right] \cr & {a_t} = \frac{{dv}}{{dt}} = 0 \cr} $$
$${a_{net}} = {a_r} = {\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre.

$$\eqalign{ & {a_r} = {\omega ^2}R \cr & {a_r} = {\left( {2\pi 2} \right)^2}R = 4{\pi ^2}{2^2}R \cr & = 4{\pi ^2}{\left( {\frac{{22}}{{44}}} \right)^4}\left( 1 \right)\,\,\left[ {\because v = \frac{{22}}{{44}}} \right] \cr & {a_t} = \frac{{dv}}{{dt}} = 0 \cr} $$
$${a_{net}} = {a_r} = {\pi ^2}m{s^{ - 2}}$$ and direction along the radius towards the centre.




