Question
A stone is attached to one end of a string and rotated in a vertical circle. If string breaks at the position of maximum tension, it will break at
A stone is attached to one end of a string and rotated in a vertical circle. If string breaks at the position of maximum tension, it will break at

A.
$$A$$
B.
$$B$$
C.
$$C$$
D.
$$D$$
Answer :
$$B$$
Solution :
When string makes an angle $$\theta $$ with the vertical in a vertical circle, then balancing the force we get
$$T - mg\cos \theta = \frac{{m{v^2}}}{l}$$
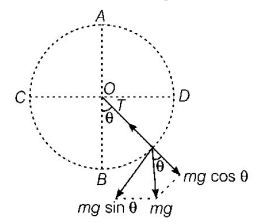
$${\text{or}}\,T = mg\cos \theta + \frac{{m{v^2}}}{l}$$
Tension is maximum when $$\cos \theta = + 1$$
i.e. $$\theta = 0$$
Thus, $$\theta $$ is zero at lowest point $$B.$$ At this point tension is maximum. So, string will break at point $$B.$$
NOTE
The critical speed of a body on circular path, $${v_c} = \sqrt {Rg} ,R = $$ radius of path.
If at the highest point, the speed is less than this, the string would become slack and the body would leave the circular path.
When string makes an angle $$\theta $$ with the vertical in a vertical circle, then balancing the force we get
$$T - mg\cos \theta = \frac{{m{v^2}}}{l}$$

$${\text{or}}\,T = mg\cos \theta + \frac{{m{v^2}}}{l}$$
Tension is maximum when $$\cos \theta = + 1$$
i.e. $$\theta = 0$$
Thus, $$\theta $$ is zero at lowest point $$B.$$ At this point tension is maximum. So, string will break at point $$B.$$
NOTE
The critical speed of a body on circular path, $${v_c} = \sqrt {Rg} ,R = $$ radius of path.
If at the highest point, the speed is less than this, the string would become slack and the body would leave the circular path.




