Question
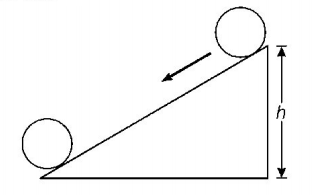
A solid cylinder of mass $$M$$ and radius $$R$$ rolls down an inclined plane of height $$h$$ without slipping. The speed of its centre of mass when it reaches the bottom is
A.
$$\sqrt {2gh} $$
B.
$$\sqrt {\frac{{4gh}}{3}} $$
C.
$$\sqrt {\frac{{3gh}}{4}} $$
D.
$$\sqrt {\frac{{4g}}{h}} $$
Answer :
$$\sqrt {\frac{{4gh}}{3}} $$
Solution :
When solid cylinder rolls down on an inclined plane, then it has both rotational and translational kinetic energy
Total kinetic energy $$K = {K_{{\text{rot}}}} + {K_{{\text{trans}}}}$$
or $$K = \frac{1}{2}I{\omega ^2} + \frac{1}{2}m{v^2}$$
where, $$I =$$ moment of inertia of solid cylinder about its axis
$$ = \frac{1}{2}m{r^2}$$
$$\eqalign{ & \therefore K = \frac{1}{2}\left( {\frac{1}{2}m{r^2}} \right){\omega ^2} + \frac{1}{2}m{v^2} \cr & = \frac{1}{4}m{v^2} + \frac{1}{2}m{v^2}\,\,\left( {{\text{as}}\,v = r\omega } \right) \cr & = \frac{3}{4}m{v^2} \cr} $$
Now, gain in $$KE =$$ loss in $$PE$$
$$\eqalign{ & \therefore \frac{3}{4}m{v^2} = mgh \cr & \Rightarrow v = \sqrt {\left( {\frac{4}{3}gh} \right)} \cr} $$
When solid cylinder rolls down on an inclined plane, then it has both rotational and translational kinetic energy

Total kinetic energy $$K = {K_{{\text{rot}}}} + {K_{{\text{trans}}}}$$
or $$K = \frac{1}{2}I{\omega ^2} + \frac{1}{2}m{v^2}$$
where, $$I =$$ moment of inertia of solid cylinder about its axis
$$ = \frac{1}{2}m{r^2}$$
$$\eqalign{ & \therefore K = \frac{1}{2}\left( {\frac{1}{2}m{r^2}} \right){\omega ^2} + \frac{1}{2}m{v^2} \cr & = \frac{1}{4}m{v^2} + \frac{1}{2}m{v^2}\,\,\left( {{\text{as}}\,v = r\omega } \right) \cr & = \frac{3}{4}m{v^2} \cr} $$
Now, gain in $$KE =$$ loss in $$PE$$
$$\eqalign{ & \therefore \frac{3}{4}m{v^2} = mgh \cr & \Rightarrow v = \sqrt {\left( {\frac{4}{3}gh} \right)} \cr} $$