Question
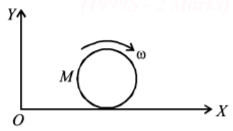
A solid cylinder of mass $$50\,kg$$ and radius $$0.5\,m$$ is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of $$2\,rev/{s^2}$$ is
A.
$$25\,N$$
B.
$$50\,N$$
C.
$$78.5\,N$$
D.
$$157\,N$$
Answer :
$$157\,N$$
Solution :
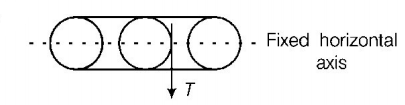
Given, $$m = 50\,kg,\,r = 0.5\,m,\,\alpha = 2\,rev/{s^2}$$
⇒ Torque produced by the tension in the string
$$ = T \times r = T \times 0.5 = \frac{T}{2}N - m\,......\left( {\text{i}} \right)$$
We know $$\tau = I\alpha \,......\left( {{\text{ii}}} \right)$$
From Eqs. (i) and (ii), $$\frac{T}{2} = I\alpha $$
$$\eqalign{ & = \left( {\frac{{M{R^2}}}{2}} \right) \times \left( {2 \times 2\pi } \right)rad/{s^2}\,\,\left[ {{\text{because }}{I_{{\text{Solid}}\,{\text{cylinder}}}} = \frac{{M{R^2}}}{2}} \right] \cr & \frac{T}{2} = \frac{{50 \times {{\left( {0.5} \right)}^2}}}{2} \times 4\pi \cr & T = 50 \times \frac{1}{4} \times 4\pi = 50\,\pi = 157\,N \cr} $$

Given, $$m = 50\,kg,\,r = 0.5\,m,\,\alpha = 2\,rev/{s^2}$$
⇒ Torque produced by the tension in the string
$$ = T \times r = T \times 0.5 = \frac{T}{2}N - m\,......\left( {\text{i}} \right)$$
We know $$\tau = I\alpha \,......\left( {{\text{ii}}} \right)$$
From Eqs. (i) and (ii), $$\frac{T}{2} = I\alpha $$
$$\eqalign{ & = \left( {\frac{{M{R^2}}}{2}} \right) \times \left( {2 \times 2\pi } \right)rad/{s^2}\,\,\left[ {{\text{because }}{I_{{\text{Solid}}\,{\text{cylinder}}}} = \frac{{M{R^2}}}{2}} \right] \cr & \frac{T}{2} = \frac{{50 \times {{\left( {0.5} \right)}^2}}}{2} \times 4\pi \cr & T = 50 \times \frac{1}{4} \times 4\pi = 50\,\pi = 157\,N \cr} $$