Releted MCQ Question on
Basic Physics >> Rotational Motion
Releted Question 1
A thin circular ring of mass $$M$$ and radius $$r$$ is rotating about its axis with a constant angular velocity $$\omega ,$$ Two objects, each of mass $$m,$$ are attached gently to the opposite ends of a diameter of the ring. The wheel now rotates with an angular velocity-
A.
$$\frac{{\omega M}}{{\left( {M + m} \right)}}$$
B.
$$\frac{{\omega \left( {M - 2m} \right)}}{{\left( {M + 2m} \right)}}$$
C.
$$\frac{{\omega M}}{{\left( {M + 2m} \right)}}$$
D.
$$\frac{{\omega \left( {M + 2m} \right)}}{M}$$
Releted Question 2
Two point masses of $$0.3 \,kg$$ and $$0.7 \,kg$$ are fixed at the ends of a rod of length $$1.4 \,m$$ and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of-
A.
$$0.42 \,m$$ from mass of $$0.3 \,kg$$
B.
$$0.70 \,m$$ from mass of $$0.7 \,kg$$
C.
$$0.98 \,m$$ from mass of $$0.3 \,kg$$
D.
$$0.98 \,m$$ from mass of $$0.7 \,kg$$
Releted Question 3
A smooth sphere $$A$$ is moving on a frictionless horizontal plane with angular speed $$\omega $$ and centre of mass velocity $$\upsilon .$$ It collides elastically and head on with an identical sphere $$B$$ at rest. Neglect friction everywhere. After the collision, their angular speeds are $${\omega _A}$$ and $${\omega _B}$$ respectively. Then-
A.
$${\omega _A} < {\omega _B}$$
B.
$${\omega _A} = {\omega _B}$$
C.
$${\omega _A} = \omega $$
D.
$${\omega _B} = \omega $$
Releted Question 4
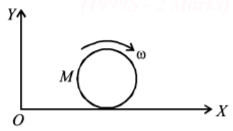
A disc of mass $$M$$ and radius $$R$$ is rolling with angular speed $$\omega $$ on a horizontal plane as shown in Figure. The magnitude of angular momentum of the disc about the origin $$O$$ is
A disc of mass $$M$$ and radius $$R$$ is rolling with angular speed $$\omega $$ on a horizontal plane as shown in Figure. The magnitude of angular momentum of the disc about the origin $$O$$ is
A.
$$\left( {\frac{1}{2}} \right)M{R^2}\omega $$
B.
$$M{R^2}\omega $$
C.
$$\left( {\frac{3}{2}} \right)M{R^2}\omega $$
D.
$$2M{R^2}\omega $$