Question
A small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
A.


B.


C.


D.


Answer :


Solution :
Since the body presses the surface with a force $$N$$ hence according to Newton's third law the surface presses the body with a force $$N.$$ The other force acting on the body is its weight $$mg.$$
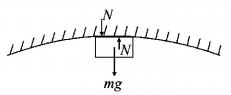
For circular motion to take place, a centripetal force is required which is provided by $$\left( {mg + N} \right).$$
$$\therefore mg + N = \frac{{m{v^2}}}{r}$$
where $$r$$ is the radius of curvature at the top.
If the surface is smooth then on applying conservation of mechanical energy, the velocity of the body is always same at the top most point. Hence, $$N$$ and $$r$$ have inverse relationship. From the figure it is clear that $$r$$ is minimum for first figure, therefore $$N$$ will be maximum.
Note : If we do not assume the surface to be smooth, we cannot reach to a conclusion.
Since the body presses the surface with a force $$N$$ hence according to Newton's third law the surface presses the body with a force $$N.$$ The other force acting on the body is its weight $$mg.$$

For circular motion to take place, a centripetal force is required which is provided by $$\left( {mg + N} \right).$$
$$\therefore mg + N = \frac{{m{v^2}}}{r}$$
where $$r$$ is the radius of curvature at the top.
If the surface is smooth then on applying conservation of mechanical energy, the velocity of the body is always same at the top most point. Hence, $$N$$ and $$r$$ have inverse relationship. From the figure it is clear that $$r$$ is minimum for first figure, therefore $$N$$ will be maximum.
Note : If we do not assume the surface to be smooth, we cannot reach to a conclusion.

