Question
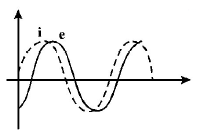
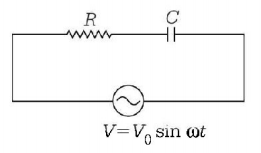
A series $$R-C$$ circuit is connected to an alternating voltage source. Consider two situations :
A series $$R-C$$ circuit is connected to an alternating voltage source. Consider two situations :
1. When capacitor is air filled.
2. When capacitor is mica filled.
Current through resistor is $$i$$ and voltage across capacitor is $$V$$ then
A.
$${V_a} < {V_b}$$
B.
$${V_a} > {V_b}$$
C.
$${i_a} > {i_b}$$
D.
$${V_a} = {V_b}$$
Answer :
$${V_a} > {V_b}$$
Solution :
Net reactive capacitance,
$${X_C} = \frac{1}{{2\pi fC}}$$
So, current in circuit, $$I = \frac{V}{Z} = \frac{V}{{\sqrt {{R^2} + {{\left( {\frac{1}{{2\pi fC}}} \right)}^2}} }}$$
$$ \Rightarrow I = \frac{{2\pi fC}}{{\sqrt {4{\pi ^2}{f^2}{C^2}{R^2} + 1} }} \times V$$
Voltage drop across capacitor, $${V_C} = I \times {X_C}$$
$$ = \frac{{2\pi fC}}{{\sqrt {4{\pi ^2}{f^2}{C^2}{R^2} + 1} }} \times \frac{1}{{2\pi fC}}$$
i.e. $${V_C} = \frac{V}{{\sqrt {4{\pi ^2}{f^2}{C^2}{R^2} + 1} }}$$
When mica is introduced, capacitance will increase hence, voltage across capacitor get decrease.
Net reactive capacitance,

$${X_C} = \frac{1}{{2\pi fC}}$$
So, current in circuit, $$I = \frac{V}{Z} = \frac{V}{{\sqrt {{R^2} + {{\left( {\frac{1}{{2\pi fC}}} \right)}^2}} }}$$
$$ \Rightarrow I = \frac{{2\pi fC}}{{\sqrt {4{\pi ^2}{f^2}{C^2}{R^2} + 1} }} \times V$$
Voltage drop across capacitor, $${V_C} = I \times {X_C}$$
$$ = \frac{{2\pi fC}}{{\sqrt {4{\pi ^2}{f^2}{C^2}{R^2} + 1} }} \times \frac{1}{{2\pi fC}}$$
i.e. $${V_C} = \frac{V}{{\sqrt {4{\pi ^2}{f^2}{C^2}{R^2} + 1} }}$$
When mica is introduced, capacitance will increase hence, voltage across capacitor get decrease.