Question
A rod $$PQ$$ of length $$L$$ moves with a uniform velocity $$v$$ parallel to a long straight wire carrying a current $$i,$$ the end $$P$$ remaining at a distance $$r$$ from the wire. The emf induced across the rod is
A.
$$\frac{{{\mu _0}i{v^2}}}{{2\pi }}\ln \left( {\frac{{r + L}}{r}} \right)$$
B.
$$\frac{{{\mu _0}{i^2}{v^2}}}{{2\pi }}\ln \left( {\frac{{{r^2} + L}}{r}} \right)$$
C.
$$\frac{{{\mu _0}iv}}{{2\pi }}\ln \left( {\frac{{r + L}}{r}} \right)$$
D.
$$\frac{{{\mu _0}iv}}{{2\pi }}\ln \left( {\frac{{{r^2} + {L^2}}}{{{L^2}}}} \right)$$
Answer :
$$\frac{{{\mu _0}iv}}{{2\pi }}\ln \left( {\frac{{r + L}}{r}} \right)$$
Solution :
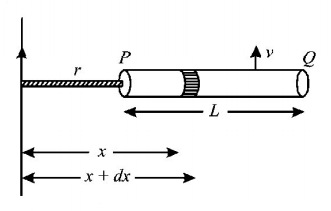
Consider a small element of length $$dx$$ of the rod at a distance $$x$$ and $$\left( {x + dx} \right)$$ from the wire.
The emf induced across the element
$$de = B\,v\,dx\,.......\left( {\text{i}} \right)$$
We know that magnetic field $$B$$ at a distance $$x$$ from a wire carrying a current $$i$$ is given by
$$B = \frac{{{\mu _0}}}{{2\pi }}.\frac{i}{x}\,.....\left( {{\text{ii}}} \right)$$
From eqs. (i) and (ii),
$$de = \frac{{{\mu _0}i}}{{2\pi x}}v\,dx\,......\left( {{\text{iii}}} \right)$$
The emf $$e$$ induced in the entire length of the rod $$PQ$$ is given by
$$\eqalign{ & e = \int {de} = \int_P^Q {\frac{{{\mu _0}}}{{2\pi }}\frac{i}{x}} v\,dx \cr & = \int_r^{r + L} {\frac{{{\mu _0}}}{{2\pi }}\frac{i}{x}} v\,dx \cr & = \frac{{{\mu _0}}}{{2\pi }}i\,v\int_r^{r + L} {\frac{{dx}}{x}} \cr & = \frac{{{\mu _0}iv}}{{2\pi }}{\log _e}\left( {\frac{{r + L}}{r}} \right) \cr} $$

Consider a small element of length $$dx$$ of the rod at a distance $$x$$ and $$\left( {x + dx} \right)$$ from the wire.
The emf induced across the element
$$de = B\,v\,dx\,.......\left( {\text{i}} \right)$$
We know that magnetic field $$B$$ at a distance $$x$$ from a wire carrying a current $$i$$ is given by
$$B = \frac{{{\mu _0}}}{{2\pi }}.\frac{i}{x}\,.....\left( {{\text{ii}}} \right)$$
From eqs. (i) and (ii),
$$de = \frac{{{\mu _0}i}}{{2\pi x}}v\,dx\,......\left( {{\text{iii}}} \right)$$
The emf $$e$$ induced in the entire length of the rod $$PQ$$ is given by
$$\eqalign{ & e = \int {de} = \int_P^Q {\frac{{{\mu _0}}}{{2\pi }}\frac{i}{x}} v\,dx \cr & = \int_r^{r + L} {\frac{{{\mu _0}}}{{2\pi }}\frac{i}{x}} v\,dx \cr & = \frac{{{\mu _0}}}{{2\pi }}i\,v\int_r^{r + L} {\frac{{dx}}{x}} \cr & = \frac{{{\mu _0}iv}}{{2\pi }}{\log _e}\left( {\frac{{r + L}}{r}} \right) \cr} $$
