Question
A rod is of length $$3\,m$$ and its mass acting per unit length is directly proportional to distance $$x$$ from its one end. The centre of gravity of the rod from that end will be at
A.
$$1.5\,m$$
B.
$$2\,m$$
C.
$$2.5\,m$$
D.
$$3\,m$$
Answer :
$$1.5\,m$$
Solution :
A rod lying along any of coordinate axes serves for us as continuous body.
Suppose a rod of mass $$M$$ and length $$L$$ is lying along the $$x$$-axis with its one end at $$x = 0$$ and the other at $$x = L.$$
Mass per unit length of the rod $$ = \frac{M}{L}$$
Hence, the mass of the element $$PQ$$ of length $$dx$$ situated at $$x = x$$ is $$dm = \frac{M}{L}dx$$
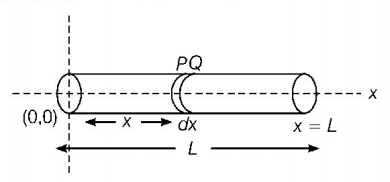
The coordinates of the element $$PQ$$ are $$\left( {x,0,0} \right).$$ Therefore, $$x$$-coordinate of centre of gravity of the rod will be
$${x_{CG}} = \frac{{\int_0^L x dm}}{{\int {dm} }} = \frac{{\int_0^L {\left( x \right)\left( {\frac{M}{L}} \right)} dx}}{M} = \frac{1}{L}\int_0^L x dx = \frac{L}{2}$$
but as given, $$L = 3\,m$$
$$\therefore {x_{CG}} = \frac{3}{2} = 1.5\,m$$
The $$y$$-coordinate of centre of gravity
$${y_{CG}} = \frac{{\int {y\,dm} }}{{\int {dm} }} = 0\,\,\left( {{\text{as}}\,y = 0} \right)$$
Similarly, $${z_{CG}} = 0$$
i.e., the coordinates of centre of gravity of the rod are $$\left( {1.5,0,0} \right)$$ or it lies at the distance $$1.5\,m$$ from one end.
A rod lying along any of coordinate axes serves for us as continuous body.
Suppose a rod of mass $$M$$ and length $$L$$ is lying along the $$x$$-axis with its one end at $$x = 0$$ and the other at $$x = L.$$
Mass per unit length of the rod $$ = \frac{M}{L}$$
Hence, the mass of the element $$PQ$$ of length $$dx$$ situated at $$x = x$$ is $$dm = \frac{M}{L}dx$$

The coordinates of the element $$PQ$$ are $$\left( {x,0,0} \right).$$ Therefore, $$x$$-coordinate of centre of gravity of the rod will be
$${x_{CG}} = \frac{{\int_0^L x dm}}{{\int {dm} }} = \frac{{\int_0^L {\left( x \right)\left( {\frac{M}{L}} \right)} dx}}{M} = \frac{1}{L}\int_0^L x dx = \frac{L}{2}$$
but as given, $$L = 3\,m$$
$$\therefore {x_{CG}} = \frac{3}{2} = 1.5\,m$$
The $$y$$-coordinate of centre of gravity
$${y_{CG}} = \frac{{\int {y\,dm} }}{{\int {dm} }} = 0\,\,\left( {{\text{as}}\,y = 0} \right)$$
Similarly, $${z_{CG}} = 0$$
i.e., the coordinates of centre of gravity of the rod are $$\left( {1.5,0,0} \right)$$ or it lies at the distance $$1.5\,m$$ from one end.