Question
A rod $$AB$$ of length $$16\,cm.$$ rests between the wall $$AD$$ and a smooth peg, $$1\,cm$$ from the wall and makes an angle $$\theta $$ with the horizontal. The value of $$\theta $$ for which the height of $$G,$$ the mid point of the rod above the peg is minimum, is :
A.
$${15^ \circ }$$
B.
$${30^ \circ }$$
C.
$${60^ \circ }$$
D.
$${75^ \circ }$$
Answer :
$${60^ \circ }$$
Solution :
We have $$AC = \sec \,\theta ,\,AG = 8$$
$$\therefore \,CG = 8 - \sec \,\theta $$ ($$C$$ being the peg)
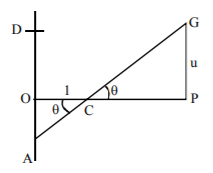
$$\eqalign{ & {\text{But }}u = CG\,\sin \,\theta = \left( {8 - \sec \,\theta } \right)\sin \,\theta \cr & u = 8\,\sin \,\theta - \tan \,\theta \cr & \frac{{du}}{{d\theta }} = 8\,\cos \,\theta - {\sec ^2}\theta , \cr & \frac{{{d^2}u}}{{d{\theta ^2}}} = - 8\,\sin \,\theta - 2\,{\sec ^2}\theta \,\tan \,\theta \cr & \frac{{du}}{{d\theta }} = 0,\,{\text{when }}{\cos ^3}\theta = \frac{1}{8},\,\cos \,\theta = \frac{1}{2}, \cr & \frac{{{d^2}u}}{{d{\theta ^2}}} > 0\left( {{\text{at }}\theta = {{60}^ \circ }} \right), \cr & \therefore \,\theta = {60^ \circ } \cr} $$
We have $$AC = \sec \,\theta ,\,AG = 8$$
$$\therefore \,CG = 8 - \sec \,\theta $$ ($$C$$ being the peg)

$$\eqalign{ & {\text{But }}u = CG\,\sin \,\theta = \left( {8 - \sec \,\theta } \right)\sin \,\theta \cr & u = 8\,\sin \,\theta - \tan \,\theta \cr & \frac{{du}}{{d\theta }} = 8\,\cos \,\theta - {\sec ^2}\theta , \cr & \frac{{{d^2}u}}{{d{\theta ^2}}} = - 8\,\sin \,\theta - 2\,{\sec ^2}\theta \,\tan \,\theta \cr & \frac{{du}}{{d\theta }} = 0,\,{\text{when }}{\cos ^3}\theta = \frac{1}{8},\,\cos \,\theta = \frac{1}{2}, \cr & \frac{{{d^2}u}}{{d{\theta ^2}}} > 0\left( {{\text{at }}\theta = {{60}^ \circ }} \right), \cr & \therefore \,\theta = {60^ \circ } \cr} $$