Question
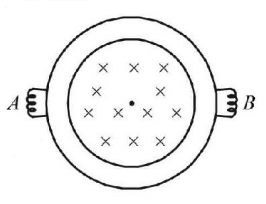
A resistance less ring has 2 bulbs $$A$$ and $$B$$ rated at $$2V,10\,W$$ and $$2V,20\,W$$ respectively. The ring encloses an ideal solenoid whose magnetic field is as shown. The radius of solenoid is $$1\,m$$ and the number of $$\frac{{{\text{turns}}}}{{{\text{length}}}} = 1000/m.$$ The current changes at rate of $$9\,A/\sec.$$ Find the value of $$P$$ if power dissipated in bulb $$B$$ is $$1.8\,P \times {10^{ - 4}}\,watt.$$
A resistance less ring has 2 bulbs $$A$$ and $$B$$ rated at $$2V,10\,W$$ and $$2V,20\,W$$ respectively. The ring encloses an ideal solenoid whose magnetic field is as shown. The radius of solenoid is $$1\,m$$ and the number of $$\frac{{{\text{turns}}}}{{{\text{length}}}} = 1000/m.$$ The current changes at rate of $$9\,A/\sec.$$ Find the value of $$P$$ if power dissipated in bulb $$B$$ is $$1.8\,P \times {10^{ - 4}}\,watt.$$

A.
4
B.
6
C.
8
D.
11
Answer :
4
Solution :
Resistance of bulb $$A = \frac{{{v^2}}}{P} = \frac{4}{{10}} = 0.4$$
Resistance of bulb $$B = \frac{{{v^2}}}{P} = 0.2$$
emf $$ = \frac{{d\phi }}{{dt}} = \frac{d}{{dt}}\left( {{\mu _0}nI \times A} \right)$$
$$\eqalign{ & = {\mu _0}n \times A \times \frac{{dI}}{{dt}} = {10^{ - 7}} \times 4\pi \times 1000 \times \pi {\left( 1 \right)^2} \times 9 \cr & v = 36 \times {10^{ - 3}} \cr & I = \frac{v}{{{R_{{\text{eq}}}}}} = \frac{{36 \times {{10}^{ - 3}}}}{{0.6}} = 6 \times {10^{ - 2}}A \cr} $$
Power dissipated through bulb $$B = {I^2}R$$
$$ = 36 \times {10^{ - 4}} \times 0.2 = 7.2 \times {10^{ - 4}}\,watt.$$
Resistance of bulb $$A = \frac{{{v^2}}}{P} = \frac{4}{{10}} = 0.4$$
Resistance of bulb $$B = \frac{{{v^2}}}{P} = 0.2$$

emf $$ = \frac{{d\phi }}{{dt}} = \frac{d}{{dt}}\left( {{\mu _0}nI \times A} \right)$$
$$\eqalign{ & = {\mu _0}n \times A \times \frac{{dI}}{{dt}} = {10^{ - 7}} \times 4\pi \times 1000 \times \pi {\left( 1 \right)^2} \times 9 \cr & v = 36 \times {10^{ - 3}} \cr & I = \frac{v}{{{R_{{\text{eq}}}}}} = \frac{{36 \times {{10}^{ - 3}}}}{{0.6}} = 6 \times {10^{ - 2}}A \cr} $$
Power dissipated through bulb $$B = {I^2}R$$
$$ = 36 \times {10^{ - 4}} \times 0.2 = 7.2 \times {10^{ - 4}}\,watt.$$
