Question
A region in the $$x$$-$$y$$ plane is bounded by the curve $$y = \sqrt {25 - {x^2}} $$ and the line $$y=0.$$ If the point $$\left( {a,\,a + 1} \right)$$ lies in the interior of the region then :
A.
$$a\, \in \,\left( { - 4,\,3} \right)$$
B.
$$a\, \in \,\left( { - \infty ,\, - 1} \right) \cup \left( {3,\, + \infty } \right)$$
C.
$$a\, \in \,\left( { - 1,\,3} \right)$$
D.
none of these
Answer :
$$a\, \in \,\left( { - 1,\,3} \right)$$
Solution :
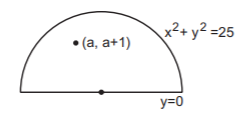
$$y = \sqrt {25 - {x^2}} ,\,y = 0$$ bound the semicircle above the $$x$$-axis.
$$\therefore \,\,a + 1 > 0{\text{ and }}{a^2} + {\left( {a + 1} \right)^2} - 25 < 0$$
Solve these and take the common values.

$$y = \sqrt {25 - {x^2}} ,\,y = 0$$ bound the semicircle above the $$x$$-axis.
$$\therefore \,\,a + 1 > 0{\text{ and }}{a^2} + {\left( {a + 1} \right)^2} - 25 < 0$$
Solve these and take the common values.