Question
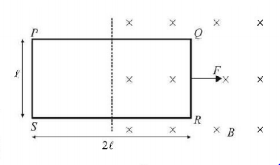
A rectangular loop $$PQRS,$$ is pulled with constant speed into a uniform transverse magnetic field by a force $$F$$ (as shown). E.m.f. induced in side $$PS$$ and potential difference between points $$P$$ and $$S$$ respectively are (Resistance of the loop = $$r$$)
A rectangular loop $$PQRS,$$ is pulled with constant speed into a uniform transverse magnetic field by a force $$F$$ (as shown). E.m.f. induced in side $$PS$$ and potential difference between points $$P$$ and $$S$$ respectively are (Resistance of the loop = $$r$$)
A.
zero, $$\frac{{Fr}}{{B\ell }}$$
B.
zero, zero
C.
zero, $$\frac{{Fr}}{{6B\ell }}$$
D.
$$\frac{{Fr}}{{6B\ell }},\frac{{Fr}}{{6B\ell }}$$
Answer :
zero, $$\frac{{Fr}}{{6B\ell }}$$
Solution :
There is no charge in flux through $$PS$$ and so induced emf will be zero. But
$$\eqalign{ & {V_P} - {V_B} = {V_Q} - {V_R} \cr & {\text{Also,}}\,F = Bil\,\,{\text{or}}\,\,i = \frac{F}{{B\ell }} \cr & \therefore {V_P} - {V_B} = {V_Q} - {V_R} = i{r_{QR}} = \frac{F}{{B\ell }} \times \frac{r}{6} = \frac{{Fr}}{{6B\ell }} \cr} $$
There is no charge in flux through $$PS$$ and so induced emf will be zero. But
$$\eqalign{ & {V_P} - {V_B} = {V_Q} - {V_R} \cr & {\text{Also,}}\,F = Bil\,\,{\text{or}}\,\,i = \frac{F}{{B\ell }} \cr & \therefore {V_P} - {V_B} = {V_Q} - {V_R} = i{r_{QR}} = \frac{F}{{B\ell }} \times \frac{r}{6} = \frac{{Fr}}{{6B\ell }} \cr} $$
