Question
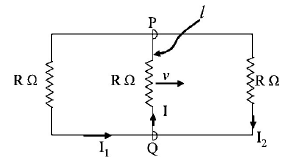
A rectangular loop has a sliding connector $$PQ$$ of length $$l$$ and resistance $$R\,\Omega $$ and it is moving with a speed $$v$$ as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents $${I_1},{I_2}$$ and $$I$$ are
A rectangular loop has a sliding connector $$PQ$$ of length $$l$$ and resistance $$R\,\Omega $$ and it is moving with a speed $$v$$ as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents $${I_1},{I_2}$$ and $$I$$ are
A.
$${I_1} = - {I_2} = \frac{{Blv}}{{6R}},I = \frac{{2Blv}}{{6R}}$$
B.
$${I_1} = {I_2} = \frac{{Blv}}{{3R}},I = \frac{{2Blv}}{{3R}}$$
C.
$${I_1} = {I_2} = I = \frac{{Blv}}{R}$$
D.
$${I_1} = {I_2} = \frac{{Blv}}{{6R}},I = \frac{{Blv}}{{3R}}$$
Answer :
$${I_1} = {I_2} = \frac{{Blv}}{{3R}},I = \frac{{2Blv}}{{3R}}$$
Solution :
Due to the movement of resistor $$R,$$ an emf equal to $$Blv$$ will be induced in it as shown in figure clearly,
$$I = {I_1} + {I_2}$$
$${\text{Also,}}\,{I_1} = {I_2}$$
Solving the circuit, we get
$$\eqalign{ & {I_1} = {I_2} = \frac{{Blv}}{{3R}} \cr & {\text{and}}\,I = 2{I_1} = \frac{{2Blv}}{{3R}} \cr} $$
Due to the movement of resistor $$R,$$ an emf equal to $$Blv$$ will be induced in it as shown in figure clearly,
$$I = {I_1} + {I_2}$$
$${\text{Also,}}\,{I_1} = {I_2}$$
Solving the circuit, we get
$$\eqalign{ & {I_1} = {I_2} = \frac{{Blv}}{{3R}} \cr & {\text{and}}\,I = 2{I_1} = \frac{{2Blv}}{{3R}} \cr} $$
