Question
A rectangular coil of length $$0.12\,m$$ and width $$0.1\,m$$ having 50 turns of wire is suspended vertically in a uniform magnetic field of strength $$0.2\,Wb/{m^2}.$$ The coil carries a current of $$2\,A.$$ If the plane of the coil is inclined at an angle of $${30^ \circ }$$ with the direction of the field, the torque required to keep the coil in stable equilibrium will be
A.
$$0.15\,Nm$$
B.
$$0.20\,Nm$$
C.
$$0.24\,Nm$$
D.
$$0.12\,Nm$$
Answer :
$$0.20\,Nm$$
Solution :
Given, $$N = 50$$
$$\eqalign{ & B = 0.2\,Wb/{m^2},I = 2A \cr & \theta = {60^ \circ },A = 0.12 \times 0.1 = 0.012\,{m^2} \cr} $$
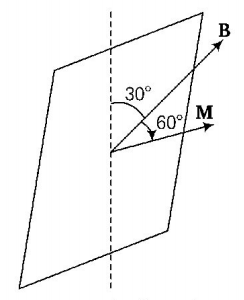
Thus, torque required to keep the coil in stable equilibrium, i.e.
$$\eqalign{ & \tau = NIAB\sin \theta = 50 \times 2 \times 0.012 \times 0.2 \times \sin {60^ \circ } \cr & = 50 \times 2 \times 0.12 \times 0.2 \times \frac{{\sqrt 3 }}{2} = 0.20\,Nm \cr} $$
Given, $$N = 50$$
$$\eqalign{ & B = 0.2\,Wb/{m^2},I = 2A \cr & \theta = {60^ \circ },A = 0.12 \times 0.1 = 0.012\,{m^2} \cr} $$

Thus, torque required to keep the coil in stable equilibrium, i.e.
$$\eqalign{ & \tau = NIAB\sin \theta = 50 \times 2 \times 0.012 \times 0.2 \times \sin {60^ \circ } \cr & = 50 \times 2 \times 0.12 \times 0.2 \times \frac{{\sqrt 3 }}{2} = 0.20\,Nm \cr} $$
