Question
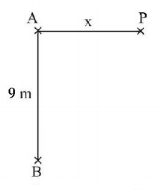
A radio transmitting station operating at a frequency of $$120\,MHz$$ has two identical antennas that radiate in phase. Antenna $$B$$ is $$9\,m$$ to the right of antenna $$A.$$ Consider point $$P$$ at a horizontal distance $$x$$ to the right of antenna $$A$$ as shown in Fig. The value of $$x$$ and order for which the constructive interference will occur at point $$P$$ is
A radio transmitting station operating at a frequency of $$120\,MHz$$ has two identical antennas that radiate in phase. Antenna $$B$$ is $$9\,m$$ to the right of antenna $$A.$$ Consider point $$P$$ at a horizontal distance $$x$$ to the right of antenna $$A$$ as shown in Fig. The value of $$x$$ and order for which the constructive interference will occur at point $$P$$ is
A.
$$x = 14.95\,m,n = 2$$
B.
$$x = 5.6\,m,n = 2$$
C.
$$x = 1.65\,m,n = 3$$
D.
$$x = 0,n = 3.6$$
Answer :
$$x = 5.6\,m,n = 2$$
Solution :
Path difference, $$\delta = BP - AP$$
$$\eqalign{ & \sqrt {{x^2} + {9^2}} - x = n\lambda \cr & \Rightarrow {x^2} + {9^2} = {n^2}{\lambda ^2} + {x^2} + 2n\lambda x \cr & \Rightarrow x = \frac{{{9^2} - {n^2}{\lambda ^2}}}{{2n\lambda }}\,\,{\text{also}}\,\,\lambda = \frac{c}{v} = \frac{{3 \times {{10}^8}}}{{120 \times {{10}^6}}} = 2.5\,m \cr & n = 1,x = 14.95\,m;n = 3,x = 1.65\,m; \cr & n = 2,x = 5.6\,m;n = 4\,\,{\text{not}}\,{\text{possible}} \cr} $$
Path difference, $$\delta = BP - AP$$
$$\eqalign{ & \sqrt {{x^2} + {9^2}} - x = n\lambda \cr & \Rightarrow {x^2} + {9^2} = {n^2}{\lambda ^2} + {x^2} + 2n\lambda x \cr & \Rightarrow x = \frac{{{9^2} - {n^2}{\lambda ^2}}}{{2n\lambda }}\,\,{\text{also}}\,\,\lambda = \frac{c}{v} = \frac{{3 \times {{10}^8}}}{{120 \times {{10}^6}}} = 2.5\,m \cr & n = 1,x = 14.95\,m;n = 3,x = 1.65\,m; \cr & n = 2,x = 5.6\,m;n = 4\,\,{\text{not}}\,{\text{possible}} \cr} $$