Question
A potentiometer wire of length $$L$$ and a resistance $$r$$ are connected in series with a battery of e.m.f. $${E_0}$$ and a resistance $${r_1}.$$ An unknown e.m.f. is balanced at a length $$l$$ of the potentiometer wire. The e.m.f. $$E$$ will be given by
A.
$$\frac{{L{E_0}r}}{{l{r_1}}}$$
B.
$$\frac{{{E_0}r}}{{\left( {r + {r_1}} \right)}} \cdot \frac{l}{L}$$
C.
$$\frac{{{E_0}l}}{L}$$
D.
$$\frac{{L{E_0}r}}{{\left( {r + {r_1}} \right)l}}$$
Answer :
$$\frac{{{E_0}r}}{{\left( {r + {r_1}} \right)}} \cdot \frac{l}{L}$$
Solution :
Consider a potentiometer wire of length $$L$$ and a resistance $$r$$ are connected in series with a battery of emf $${{E_0}}$$ and a resistance $${{r_1}}$$ as shown in figure. Current in wire $$AB = \frac{{{E_0}}}{{{r_1} + r}}$$
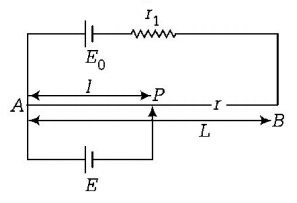
Potential gradient,
$$x = \frac{{Ir}}{L} = \left[ {\frac{{{E_0}}}{{{r_1} + r}}} \right]\frac{r}{L}$$
emf produced across $$E$$ will be given by
$$E = x \cdot l = \left[ {\frac{{{E_0}r}}{{{r_1} + r}}} \right]\frac{l}{L}$$
Consider a potentiometer wire of length $$L$$ and a resistance $$r$$ are connected in series with a battery of emf $${{E_0}}$$ and a resistance $${{r_1}}$$ as shown in figure. Current in wire $$AB = \frac{{{E_0}}}{{{r_1} + r}}$$

Potential gradient,
$$x = \frac{{Ir}}{L} = \left[ {\frac{{{E_0}}}{{{r_1} + r}}} \right]\frac{r}{L}$$
emf produced across $$E$$ will be given by
$$E = x \cdot l = \left[ {\frac{{{E_0}r}}{{{r_1} + r}}} \right]\frac{l}{L}$$
