Question
A pole stands vertically inside a triangular park $$\Delta ABC.$$ If the angle of elevation of the top of the pole from each corner of the park is same, then in $$\Delta ABC$$ the foot of the pole is at the
A.
centroid
B.
circumcentre
C.
incentre
D.
orthocentre
Answer :
circumcentre
Solution :
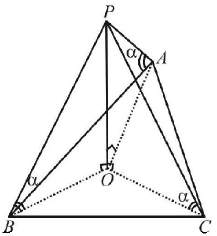
Let $$OP =$$ Pole,
$$\eqalign{ & \angle PAO = \angle PBO = \angle PCQ = \alpha \cr & \frac{{OP}}{{OB}} = \tan \alpha \cr & \Rightarrow \,\,OB = OP\cot \alpha \,\,\,\,\,\,.....\left( 1 \right) \cr} $$
$$\eqalign{ & {\text{Similarly}}\,\,OA = OP\cot \alpha \,\,\,\,\,.....\left( 2 \right) \cr & {\text{Similarly}}\,\,OC = OP\cot \alpha \,\,\,\,\,.....\left( 3 \right) \cr} $$
From (1), (2) and (3), $$OA = OB = OC$$
⇒ $$O$$ is the point of circumcentre of the triangle $$ABC.$$

Let $$OP =$$ Pole,
$$\eqalign{ & \angle PAO = \angle PBO = \angle PCQ = \alpha \cr & \frac{{OP}}{{OB}} = \tan \alpha \cr & \Rightarrow \,\,OB = OP\cot \alpha \,\,\,\,\,\,.....\left( 1 \right) \cr} $$
$$\eqalign{ & {\text{Similarly}}\,\,OA = OP\cot \alpha \,\,\,\,\,.....\left( 2 \right) \cr & {\text{Similarly}}\,\,OC = OP\cot \alpha \,\,\,\,\,.....\left( 3 \right) \cr} $$
From (1), (2) and (3), $$OA = OB = OC$$
⇒ $$O$$ is the point of circumcentre of the triangle $$ABC.$$