Question
A point light source is moving with a constant velocity $$v$$ inside a transparent thin spherical shell of radius $$R,$$ which is filled with a transparent liquid. If at $$t = 0$$ light source is at the centre of the sphere, then at what time a thin dark ring will be visible for an observer outside the sphere. The refractive index of liquid with respect to that of shell is $$\sqrt 2 .$$
A.
$$\frac{R}{{\sqrt 2 V}}$$
B.
$$\frac{R}{{2V}}$$
C.
$$\frac{R}{{3V}}$$
D.
$$\frac{R}{{\sqrt 3 V}}$$
Answer :
$$\frac{R}{{\sqrt 2 V}}$$
Solution :
This dark ring will be visible if ray from source gets total internal reflection from the spherical shell.
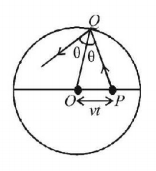
Let the source at any instant be at point $$P$$ then at point $$Q$$ ray will be totally reflected if $$\theta $$ is equal to or greater than critical angle. If $$QP$$ is equal to $$x,$$ then
$$z = \cos \theta = \frac{{{R^2} + {x^2} - {v^2}{t^2}}}{{2Rx}}$$
For $$\theta $$ to be minimum
$$\eqalign{ & \frac{{dz}}{{dx}} = \frac{{2x\left( {2Rx} \right) - 2R\left( {{R^2} + {x^2} - {v^2}{t^2}} \right)}}{{4{R^2}{x^2}}} = 0 \cr & \Rightarrow x = \sqrt {{R^2} - {v^2}{t^2}} \cr & {\text{So,}}\,\cos \theta = \frac{{2\left( {{R^2} - {v^2}{t^2}} \right)}}{{2R\sqrt {{R^2} - {v^2}{t^2}} }} = \frac{{\sqrt {{R^2} - {v^2}{t^2}} }}{R} \cr} $$
For no light come out, $$\sin \theta \geqslant \frac{1}{{\sqrt 2 }}\,\,{\text{or}}\,\,\theta \geqslant {45^ \circ }$$
$$\eqalign{ & \frac{{\sqrt {{R^2} - {v^2}{t^2}} }}{R} = \frac{1}{{\sqrt 2 }}; \cr & t = \frac{R}{{\sqrt 2 V}} \cr} $$
This dark ring will be visible if ray from source gets total internal reflection from the spherical shell.

Let the source at any instant be at point $$P$$ then at point $$Q$$ ray will be totally reflected if $$\theta $$ is equal to or greater than critical angle. If $$QP$$ is equal to $$x,$$ then
$$z = \cos \theta = \frac{{{R^2} + {x^2} - {v^2}{t^2}}}{{2Rx}}$$
For $$\theta $$ to be minimum
$$\eqalign{ & \frac{{dz}}{{dx}} = \frac{{2x\left( {2Rx} \right) - 2R\left( {{R^2} + {x^2} - {v^2}{t^2}} \right)}}{{4{R^2}{x^2}}} = 0 \cr & \Rightarrow x = \sqrt {{R^2} - {v^2}{t^2}} \cr & {\text{So,}}\,\cos \theta = \frac{{2\left( {{R^2} - {v^2}{t^2}} \right)}}{{2R\sqrt {{R^2} - {v^2}{t^2}} }} = \frac{{\sqrt {{R^2} - {v^2}{t^2}} }}{R} \cr} $$
For no light come out, $$\sin \theta \geqslant \frac{1}{{\sqrt 2 }}\,\,{\text{or}}\,\,\theta \geqslant {45^ \circ }$$
$$\eqalign{ & \frac{{\sqrt {{R^2} - {v^2}{t^2}} }}{R} = \frac{1}{{\sqrt 2 }}; \cr & t = \frac{R}{{\sqrt 2 V}} \cr} $$

