Question
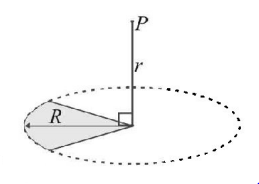
A plastic disc is charged on one side with a uniform surface charge density $$\sigma $$ and then three quadrant of the disk are removed. The remaining quadrant is shown in figure, with $$V = 0$$ at infinity, the potential due to the remaining quadrant at point $$P$$ is
A plastic disc is charged on one side with a uniform surface charge density $$\sigma $$ and then three quadrant of the disk are removed. The remaining quadrant is shown in figure, with $$V = 0$$ at infinity, the potential due to the remaining quadrant at point $$P$$ is
A.
$$\frac{\sigma }{{2{ \in _0}}}\left[ {{{\left( {{r^2} + R} \right)}^{\frac{1}{2}}} - r} \right]$$
B.
$$\frac{\sigma }{{2{ \in _0}}}\left[ {R - r} \right]$$
C.
$$\frac{\sigma }{{8{ \in _0}}}\left[ {{{\left( {{r^2} + {R^2}} \right)}^{\frac{1}{2}}} - r} \right]$$
D.
None of these
Answer :
$$\frac{\sigma }{{8{ \in _0}}}\left[ {{{\left( {{r^2} + {R^2}} \right)}^{\frac{1}{2}}} - r} \right]$$
Solution :
The potential at $$P$$ due to whole disc is
$$V = \frac{\sigma }{{2{ \in _0}}}\left[ {\sqrt {{R^2} + {r^2} - r} } \right].$$
Now potential due to quarter disc,
$$V = \frac{V}{4} = \frac{\sigma }{{8{ \in _0}}}\left[ {\sqrt {{R^2} + {r^2}} - r} \right].$$
The potential at $$P$$ due to whole disc is
$$V = \frac{\sigma }{{2{ \in _0}}}\left[ {\sqrt {{R^2} + {r^2} - r} } \right].$$
Now potential due to quarter disc,
$$V = \frac{V}{4} = \frac{\sigma }{{8{ \in _0}}}\left[ {\sqrt {{R^2} + {r^2}} - r} \right].$$