Question
A particle of mass $$m$$ and charge $$q$$ enters a region of magnetic field (as shown) with speed $$v.$$ There is a region in which the magnetic field is absent, as shown. The particle after entering the region collides elastically with a rigid wall. Time after which the velocity of particle becomes antiparallel to its initial velocity is
A particle of mass $$m$$ and charge $$q$$ enters a region of magnetic field (as shown) with speed $$v.$$ There is a region in which the magnetic field is absent, as shown. The particle after entering the region collides elastically with a rigid wall. Time after which the velocity of particle becomes antiparallel to its initial velocity is
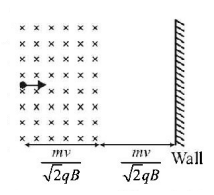
A.
$$\frac{m}{{2qB}}\left( {\pi + 4} \right)$$
B.
$$\frac{m}{{qB}}\left( {\pi + 2} \right)$$
C.
$$\frac{m}{{4qB}}\left( {\pi + 2} \right)$$
D.
$$\frac{m}{{4qB}}\left( {2\pi + 3} \right)$$
Answer :
$$\frac{m}{{2qB}}\left( {\pi + 4} \right)$$
Solution :
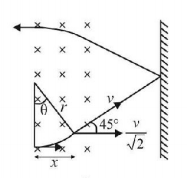
$$\eqalign{ & r = \frac{{mv}}{{qB}} \cr & \sin \theta = \frac{x}{r} = \frac{{\frac{{mv}}{{\sqrt 2 qB}}}}{{\frac{{mv}}{{qB}}}} = \frac{1}{{\sqrt 2 }} \cr & {\text{or}}\,\,\theta = \frac{\pi }{4} \cr} $$
Time to complete the circle $$\left( {2\pi } \right),T = \frac{{2\pi m}}{{qB}}$$
∴ time taken to traverses $$\frac{\pi }{4},t = \frac{{\pi m}}{{4qB}}$$
Time taken to travel horizontal distance
$${t_1} = \frac{{\frac{{mv}}{{\sqrt 2 qB}}}}{{\frac{v}{{\sqrt 2 }}}} = \frac{m}{{qB}}$$
Total time taken $$ = 2t + 2{t_1} = \frac{m}{{2qB}}\left( {\pi + 4} \right)$$

$$\eqalign{ & r = \frac{{mv}}{{qB}} \cr & \sin \theta = \frac{x}{r} = \frac{{\frac{{mv}}{{\sqrt 2 qB}}}}{{\frac{{mv}}{{qB}}}} = \frac{1}{{\sqrt 2 }} \cr & {\text{or}}\,\,\theta = \frac{\pi }{4} \cr} $$
Time to complete the circle $$\left( {2\pi } \right),T = \frac{{2\pi m}}{{qB}}$$
∴ time taken to traverses $$\frac{\pi }{4},t = \frac{{\pi m}}{{4qB}}$$
Time taken to travel horizontal distance
$${t_1} = \frac{{\frac{{mv}}{{\sqrt 2 qB}}}}{{\frac{v}{{\sqrt 2 }}}} = \frac{m}{{qB}}$$
Total time taken $$ = 2t + 2{t_1} = \frac{m}{{2qB}}\left( {\pi + 4} \right)$$