Question
A particle is acted by a force $$F= kx,$$ where $$k$$ is a $$+ve$$ constant. Its potential energy at $$x = 0$$ is zero. Which curve correctly represents the variation of potential energy of the block with respect to $$x$$
A.
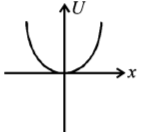

B.
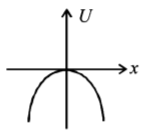

C.
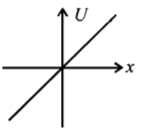

D.
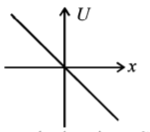

Answer :


Solution :
We know that $$\Delta U = - W$$ for conservative forces
$$\eqalign{ & \Delta U = - \int_0^x {Fdx} \;{\text{or }}\Delta U = - \int_0^x {k\,xdx\,\,} \cr & \Rightarrow {U_{\left( x \right)}} - {U_{\left( 0 \right)}} = - \frac{{k{x^2}}}{2} \cr & {\text{Given }}{U_{\left( 0 \right)}} = 0\,\,\,\,\,\,\,\,\,{U_{\left( x \right)}} = - \frac{{k{x^2}}}{2} \cr} $$
We know that $$\Delta U = - W$$ for conservative forces
$$\eqalign{ & \Delta U = - \int_0^x {Fdx} \;{\text{or }}\Delta U = - \int_0^x {k\,xdx\,\,} \cr & \Rightarrow {U_{\left( x \right)}} - {U_{\left( 0 \right)}} = - \frac{{k{x^2}}}{2} \cr & {\text{Given }}{U_{\left( 0 \right)}} = 0\,\,\,\,\,\,\,\,\,{U_{\left( x \right)}} = - \frac{{k{x^2}}}{2} \cr} $$