Question
A particle free to move along the $$x$$-axis has potential energy given by $$U\left( x \right) = k\left[ {1 - \exp \left( { - {x^2}} \right)} \right]$$ for $$ - \infty \leqslant x \leqslant + \infty ,$$ where $$k$$ is a positive constant of appropriate dimensions. Then
A.
at points away from the origin, the particle is in unstable equilibrium
B.
for any finite nonzero value of $$x,$$ there is a force directed away from the origin
C.
if its total mechanical energy is $$\frac{k}{2},$$ it has its minimum kinetic
energy at the origin.
D.
for small displacements from $$x = 0,$$ the motion is simple harmonic
Answer :
for small displacements from $$x = 0,$$ the motion is simple harmonic
Solution :
Let us plot the graph of the mathematical equation $$U\left( x \right) = K\left[ {1 - {e^ - }{{^x}^{^2}}} \right],F = \frac{{dU}}{{dx}} = 2kx{e^{ - x}}^{^2}$$
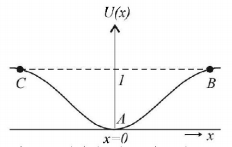
From the graph it is clear that the potential energy is minimum at $$x = 0.$$ Therefore, $$x = 0$$ is the state of stable equilibrium. Now if we displace the particle from $$x = 0$$ then for displacements the particle tends to regain the position $$x = 0$$ with a force $$F = \frac{{2kx}}{{{e^x}^{^2}}}.$$ Therefore for small values of $$x$$ we have $$F \propto x.$$
Let us plot the graph of the mathematical equation $$U\left( x \right) = K\left[ {1 - {e^ - }{{^x}^{^2}}} \right],F = \frac{{dU}}{{dx}} = 2kx{e^{ - x}}^{^2}$$

From the graph it is clear that the potential energy is minimum at $$x = 0.$$ Therefore, $$x = 0$$ is the state of stable equilibrium. Now if we displace the particle from $$x = 0$$ then for displacements the particle tends to regain the position $$x = 0$$ with a force $$F = \frac{{2kx}}{{{e^x}^{^2}}}.$$ Therefore for small values of $$x$$ we have $$F \propto x.$$