Question
A mirror and a source of light are situated at the origin $$O$$ and at a point on $$OX$$ respectively. A ray of light from the source strikes the mirror and is reflected. If the direction ratios of the normal to the plane are $$1,\, – 1,\, 1,$$ then direction cosines of the reflected rays are :
A.
$$\frac{1}{3},\,\frac{2}{3},\,\frac{2}{3}$$
B.
$$ - \frac{1}{3},\,\frac{2}{3},\,\frac{2}{3}$$
C.
$$ - \frac{1}{3},\,\frac{2}{3},\, - \frac{2}{3}$$
D.
$$ - \frac{1}{3},\, - \frac{2}{3},\,\frac{2}{3}$$
Answer :
$$ - \frac{1}{3},\, - \frac{2}{3},\,\frac{2}{3}$$
Solution :
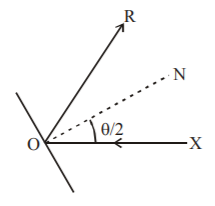
Let the ray of light comes along $$x$$-axis and strikes the mirror at the origin.
Direction cosines of normal are
$$\frac{1}{{\sqrt 3 }},\, - \frac{1}{{\sqrt 3 }},\,\frac{1}{{\sqrt 3 }}{\text{ so, }}\cos \frac{\theta }{2} = \frac{1}{{\sqrt 3 }}$$
Let the reflected ray has direction cosines $$l,\,m,\,n$$ then
$$\eqalign{ & \frac{{l + 1}}{{2\,\cos \frac{\theta }{2}}} = \frac{1}{{\sqrt 3 }} \Rightarrow l = \frac{2}{3} - 1 = - \frac{1}{3} \cr & \frac{{m + 0}}{{2\,\cos \frac{\theta }{2}}} = - \frac{1}{{\sqrt 3 }} \Rightarrow m = - \frac{2}{3} \cr & \frac{{n + 0}}{{2\,\cos \frac{\theta }{2}}} = \frac{1}{{\sqrt 3 }} \Rightarrow n = \frac{2}{3} \cr} $$

Let the ray of light comes along $$x$$-axis and strikes the mirror at the origin.
Direction cosines of normal are
$$\frac{1}{{\sqrt 3 }},\, - \frac{1}{{\sqrt 3 }},\,\frac{1}{{\sqrt 3 }}{\text{ so, }}\cos \frac{\theta }{2} = \frac{1}{{\sqrt 3 }}$$
Let the reflected ray has direction cosines $$l,\,m,\,n$$ then
$$\eqalign{ & \frac{{l + 1}}{{2\,\cos \frac{\theta }{2}}} = \frac{1}{{\sqrt 3 }} \Rightarrow l = \frac{2}{3} - 1 = - \frac{1}{3} \cr & \frac{{m + 0}}{{2\,\cos \frac{\theta }{2}}} = - \frac{1}{{\sqrt 3 }} \Rightarrow m = - \frac{2}{3} \cr & \frac{{n + 0}}{{2\,\cos \frac{\theta }{2}}} = \frac{1}{{\sqrt 3 }} \Rightarrow n = \frac{2}{3} \cr} $$