Question
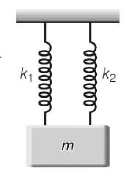
A mass is suspended separately by two springs of spring constants $${k_1}$$ and $${k_2}$$ in successive order. The time periods of oscillations in the two cases are $${T_1}$$ and $${T_2}$$ respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is $$T.$$ The correct relation is
A mass is suspended separately by two springs of spring constants $${k_1}$$ and $${k_2}$$ in successive order. The time periods of oscillations in the two cases are $${T_1}$$ and $${T_2}$$ respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is $$T.$$ The correct relation is
A.
$${T^2} = T_1^2 + T_2^2$$
B.
$${T^{ - 2}} = T_1^{ - 2} + T_2^{ - 2}$$
C.
$${T^{ - 1}} = T_1^{ - 1} + T_2^{ - 1}$$
D.
$$T = {T_1} + {T_2}$$
Answer :
$${T^{ - 2}} = T_1^{ - 2} + T_2^{ - 2}$$
Solution :
Calculate the effective force constant of parallel spring, then by putting the values of time period $$T = 2\pi \sqrt {\frac{M}{K}} ,$$ we get the new time period of spring.
We can write time period for a vertical spring-block system as
$$T = 2\pi \sqrt {\frac{l}{g}} $$
Here, $$l$$ is extension in the spring when the mass $$m$$ is suspended from the spring.
This can be seen as under :
$$\eqalign{ & kl = mg\,\,\left( {{\text{in equilibrium position}}} \right) \cr & \Rightarrow \frac{m}{k} = \frac{l}{g} \cr & \therefore T = 2\pi \sqrt {\frac{m}{k}} \cr & \therefore {T_1} = 2\pi \sqrt {\frac{m}{{{k_1}}}} \cr & \Rightarrow {k_1} = 4{\pi ^2}\frac{m}{{T_1^2}}\,......\left( {\text{i}} \right) \cr & {T_2} = 2\pi \sqrt {\frac{m}{{{k_2}}}} \cr & \Rightarrow {k_2} = 4{\pi ^2}\frac{m}{{T_2^2}}\,......\left( {{\text{ii}}} \right) \cr} $$
Since, springs are in parallel, effective force constant
$$\eqalign{ & k = {k_1} + {k_2} \cr & \therefore T = 2\pi \sqrt {\frac{m}{{{k_1} + {k_2}}}} \cr & \Rightarrow {k_1} + {k_2} = 4{\pi ^2}\frac{m}{{{T^2}}}\,......\left( {{\text{iii}}} \right) \cr} $$
Substituting values of $${k_1}$$ and $${k_2}$$ from Eqs. (i) and (ii) in Eq. (iii), we get
$$\eqalign{ & 4{\pi ^2}\frac{m}{{T_1^2}} + 4{\pi ^2}\frac{m}{{T_2^2}} = 4{\pi ^2}\frac{m}{{{T^2}}} \cr & \Rightarrow \frac{1}{{{T^2}}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}} \cr & {\text{or}}\,\,{T^{ - 2}} = T_1^{ - 2} + T_2^{ - 2} \cr} $$
Calculate the effective force constant of parallel spring, then by putting the values of time period $$T = 2\pi \sqrt {\frac{M}{K}} ,$$ we get the new time period of spring.
We can write time period for a vertical spring-block system as
$$T = 2\pi \sqrt {\frac{l}{g}} $$
Here, $$l$$ is extension in the spring when the mass $$m$$ is suspended from the spring.
This can be seen as under :
$$\eqalign{ & kl = mg\,\,\left( {{\text{in equilibrium position}}} \right) \cr & \Rightarrow \frac{m}{k} = \frac{l}{g} \cr & \therefore T = 2\pi \sqrt {\frac{m}{k}} \cr & \therefore {T_1} = 2\pi \sqrt {\frac{m}{{{k_1}}}} \cr & \Rightarrow {k_1} = 4{\pi ^2}\frac{m}{{T_1^2}}\,......\left( {\text{i}} \right) \cr & {T_2} = 2\pi \sqrt {\frac{m}{{{k_2}}}} \cr & \Rightarrow {k_2} = 4{\pi ^2}\frac{m}{{T_2^2}}\,......\left( {{\text{ii}}} \right) \cr} $$
Since, springs are in parallel, effective force constant
$$\eqalign{ & k = {k_1} + {k_2} \cr & \therefore T = 2\pi \sqrt {\frac{m}{{{k_1} + {k_2}}}} \cr & \Rightarrow {k_1} + {k_2} = 4{\pi ^2}\frac{m}{{{T^2}}}\,......\left( {{\text{iii}}} \right) \cr} $$
Substituting values of $${k_1}$$ and $${k_2}$$ from Eqs. (i) and (ii) in Eq. (iii), we get
$$\eqalign{ & 4{\pi ^2}\frac{m}{{T_1^2}} + 4{\pi ^2}\frac{m}{{T_2^2}} = 4{\pi ^2}\frac{m}{{{T^2}}} \cr & \Rightarrow \frac{1}{{{T^2}}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}} \cr & {\text{or}}\,\,{T^{ - 2}} = T_1^{ - 2} + T_2^{ - 2} \cr} $$