Question
A magnetic moment of $$1.73\,BM$$ will be shown by one among the following
A.
$${\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }}$$
B.
$${\left[ {Ni{{\left( {CN} \right)}_4}} \right]^{2 - }}$$
C.
$$TiC{l_4}$$
D.
$${\left[ {CoC{l_6}} \right]^{4 - }}$$
Answer :
$${\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }}$$
Solution :
Magnetic moment, $$\mu $$ is related with number of unpaired electrons as
$$\eqalign{ & \mu = \sqrt {n\left( {n + 2} \right)} \,BM \cr & {\left( {1.73} \right)^2} = n\left( {n + 2} \right) \cr} $$
On solving $$n=1$$
Thus, the complex/compound having one unpaired electron exhibit a magnetic moment of $$1.73\,BM.$$
$$\eqalign{ & \left( {\text{A}} \right){\text{In}}{\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }} \cr & C{u^{2 + }} = \left[ {Ar} \right]3{d^9} \cr} $$
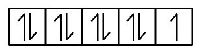
( Although in the presence of strong field ligand $$N{H_3},$$ the unpaired electron gets excited to higher energy level but it still remains unpaired ).
$$\eqalign{ & \left( {\text{B}} \right){\text{In}}{\left[ {Ni{{\left( {CN} \right)}_4}} \right]^{2 - }} \cr & N{i^{2 + }} = \left[ {Ar} \right]3{d^8} \cr} $$
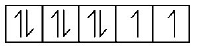
But $$C{N^ - }$$ being strong field ligand pair up the unpaired electrons and hence in this complex, number of unpaired electrons = 0.
$$\eqalign{ & \left( {\text{C}} \right){\text{In}}\left[ {TiC{l_4}} \right] \cr & T{i^{4 + }} = \left[ {Ar} \right] \cr} $$
no unpaired electron.
$$\eqalign{ & \left( {\text{D}} \right){\text{In}}{\left[ {CoC{l_6}} \right]^{4 - }} \cr & C{o^{2 + }} = \left[ {Ar} \right]3{d^7} \cr} $$
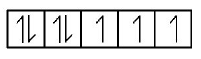
It contains three unpaired electrons.
Thus, $${\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }}$$ is the complex that exhibits a magnetic moment $$1.73\,BM.$$
Magnetic moment, $$\mu $$ is related with number of unpaired electrons as
$$\eqalign{ & \mu = \sqrt {n\left( {n + 2} \right)} \,BM \cr & {\left( {1.73} \right)^2} = n\left( {n + 2} \right) \cr} $$
On solving $$n=1$$
Thus, the complex/compound having one unpaired electron exhibit a magnetic moment of $$1.73\,BM.$$
$$\eqalign{ & \left( {\text{A}} \right){\text{In}}{\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }} \cr & C{u^{2 + }} = \left[ {Ar} \right]3{d^9} \cr} $$

( Although in the presence of strong field ligand $$N{H_3},$$ the unpaired electron gets excited to higher energy level but it still remains unpaired ).
$$\eqalign{ & \left( {\text{B}} \right){\text{In}}{\left[ {Ni{{\left( {CN} \right)}_4}} \right]^{2 - }} \cr & N{i^{2 + }} = \left[ {Ar} \right]3{d^8} \cr} $$

But $$C{N^ - }$$ being strong field ligand pair up the unpaired electrons and hence in this complex, number of unpaired electrons = 0.
$$\eqalign{ & \left( {\text{C}} \right){\text{In}}\left[ {TiC{l_4}} \right] \cr & T{i^{4 + }} = \left[ {Ar} \right] \cr} $$
no unpaired electron.
$$\eqalign{ & \left( {\text{D}} \right){\text{In}}{\left[ {CoC{l_6}} \right]^{4 - }} \cr & C{o^{2 + }} = \left[ {Ar} \right]3{d^7} \cr} $$

It contains three unpaired electrons.
Thus, $${\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]^{2 + }}$$ is the complex that exhibits a magnetic moment $$1.73\,BM.$$