Question
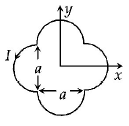
A loop carrying current $$I$$ lies in the $$x - y$$ plane as shown in the figure. The unit vector $${\hat k}$$ is coming out of the plane of the paper. The magnetic moment of the current loop is
A loop carrying current $$I$$ lies in the $$x - y$$ plane as shown in the figure. The unit vector $${\hat k}$$ is coming out of the plane of the paper. The magnetic moment of the current loop is
A.
$${a^2}I\hat k$$
B.
$$\left( {\frac{\pi }{2} + 1} \right){a^2}I\hat k$$
C.
$$ - \left( {\frac{\pi }{2} + 1} \right){a^2}I\hat k$$
D.
$$\left( {2\pi + 1} \right){a^2}I\hat k$$
Answer :
$$\left( {\frac{\pi }{2} + 1} \right){a^2}I\hat k$$
Solution :
The magnetic moment of a current carrying loop is given by $$\overrightarrow M = NI\overrightarrow A $$
Here $$N = 1,\,A = {a^2} + 2\pi {\left( {\frac{a}{2}} \right)^2} = {a^2}\left[ {1 + \frac{\pi }{2}} \right],$$ the direction is towards positive $$z$$-axis.
$$\therefore \overrightarrow M = I{a^2}\left[ {1 + \frac{\pi }{2}} \right]\hat k$$
The magnetic moment of a current carrying loop is given by $$\overrightarrow M = NI\overrightarrow A $$
Here $$N = 1,\,A = {a^2} + 2\pi {\left( {\frac{a}{2}} \right)^2} = {a^2}\left[ {1 + \frac{\pi }{2}} \right],$$ the direction is towards positive $$z$$-axis.
$$\therefore \overrightarrow M = I{a^2}\left[ {1 + \frac{\pi }{2}} \right]\hat k$$