Question
A line $$PQ$$ meets the parabola $${y^2} = 4ax$$ in $$R$$ such that $$PQ$$ is bisected at $$R$$. If the coordinates of $$P$$ are $$\left( {{x_1},\,{y_1}} \right)$$ then the locus of $$Q$$ is the parabola :
A.
$${\left( {y + {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
B.
$${\left( {y - {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
C.
$${\left( {y + {y_1}} \right)^2} = 8a\left( {x - {x_1}} \right)$$
D.
None of these
Answer :
$${\left( {y + {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
Solution :
Let the coordinates of $$Q$$ be $$\left( {h,\,k} \right).$$ Since the point $$R$$ lies on the parabola. let its coordinates be $$\left( {a{t^2},\,2at} \right).$$
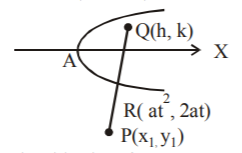
Since $$R$$ is mid point of $$PQ,$$
$$\eqalign{ & \therefore \,a{t^2} = \frac{{{x_1} + h}}{2}{\text{ and }}2at = \frac{{{y_1} + k}}{2} \cr & \Rightarrow {t^2} = \frac{{{x_1} + h}}{{2a}}{\text{ and }}t = \frac{{{y_1} + k}}{{4a}} \cr} $$
Equating the two values of $$t,$$ we get
$${\left( {\frac{{{y_1} + k}}{{4a}}} \right)^2} = \frac{{{x_1} + h}}{{2a}}\, \Rightarrow {\left( {{y_1} + k} \right)^2} = 8a\left( {{x_1} + h} \right)$$
Hence, locus of $$Q\left( {h,\,k} \right)$$ is $${\left( {y + {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$
Let the coordinates of $$Q$$ be $$\left( {h,\,k} \right).$$ Since the point $$R$$ lies on the parabola. let its coordinates be $$\left( {a{t^2},\,2at} \right).$$
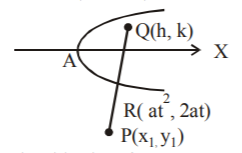
Since $$R$$ is mid point of $$PQ,$$
$$\eqalign{ & \therefore \,a{t^2} = \frac{{{x_1} + h}}{2}{\text{ and }}2at = \frac{{{y_1} + k}}{2} \cr & \Rightarrow {t^2} = \frac{{{x_1} + h}}{{2a}}{\text{ and }}t = \frac{{{y_1} + k}}{{4a}} \cr} $$
Equating the two values of $$t,$$ we get
$${\left( {\frac{{{y_1} + k}}{{4a}}} \right)^2} = \frac{{{x_1} + h}}{{2a}}\, \Rightarrow {\left( {{y_1} + k} \right)^2} = 8a\left( {{x_1} + h} \right)$$
Hence, locus of $$Q\left( {h,\,k} \right)$$ is $${\left( {y + {y_1}} \right)^2} = 8a\left( {x + {x_1}} \right)$$