A lamp is $$50\,ft$$  above the ground. A ball is dropped from the same height from a point $$30\,ft$$  away from the light pole. If ball falls a distance $$s = 16{t^2}\,ft$$   in $$t$$ seconds, then the speed of the shadow of the ball moving along the ground $$\frac{1}{2}\,s$$  later is :

Solution :

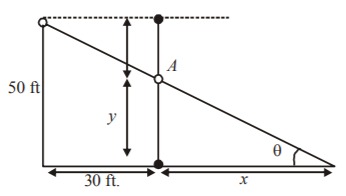
At time $$t,$$ ball drops $$16{t^2}\,ft$$   distance. Therefore, $$y = 50 - 16{t^2}.....\left( 1 \right)$$
Point $$A$$ is the position of the falling ball at some time $$t.$$ So, $$\frac{{dy}}{{dt}} = - 32t$$
From the figure, $$\tan \,\theta = \frac{y}{x} = \frac{{50}}{{30 + x}}{\text{ or }}y = \left( {\frac{{50}}{{30 + x}}} \right).x$$
$$\eqalign{ & \therefore \,\frac{{dy}}{{dt}} = \frac{d}{{dt}}\left( {\frac{{50}}{{30 + x}}} \right) = \frac{{1500}}{{{{\left( {30 + x} \right)}^2}}}.\frac{{dx}}{{dt}} \cr & {\text{or }}\frac{{dx}}{{dt}} = \frac{{\left( {30 + {x^2}} \right)}}{{1500}}\left( { - 32t} \right) \cr & {\text{When }}f = \frac{1}{2},\,y = 46\,\,\,\,\,\,\,\left[ {{\text{using}}\left( 1 \right)} \right] \cr & {\text{and }}x = 345\,\,\,\,\,\,\,\left[ {{\text{using}}\left( 2 \right)} \right] \cr & \therefore \,\frac{{dx}}{{dt}} = - 16\frac{{{{\left( {375} \right)}^2}}}{{1500}} = - 1500\,{\text{ft/s}} \cr} $$