Question
A granite rod of $$60\,cm$$ length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is $$2.7 \times {10^3}kg/{m^3}$$ and its Young's modulus is $$9.27 \times {10^{10}}Pa.$$ What will be the fundamental frequency of the longitudinal vibrations?
A.
$$5\,kHz$$
B.
$$2.5\,kHz$$
C.
$$10\,kHz$$
D.
$$7.5\,kHz$$
Answer :
$$5\,kHz$$
Solution :
In solids, Velocity of wave $$V = \sqrt {\frac{Y}{\rho }} = \sqrt {\frac{{9.27 \times {{10}^{10}}}}{{2.7 \times {{10}^3}}}} $$
$$v = 5.85 \times {10^3}m/\sec $$
Since rod is clamped at middle fundamental wave shape is as follow
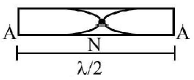
$$\eqalign{ & \frac{\lambda }{2} = L \cr & \Rightarrow \,\,\lambda = 2\,L \cr & \lambda = 1.2\,m\left( {\because \,\,L = 60\,cm = 0.6\,m\left( {{\text{given}}} \right)} \right) \cr & {\text{Using, }}v = f\lambda \cr & \Rightarrow \,\,f = \frac{v}{\lambda } = \frac{{5.85 \times {{10}^3}}}{{1.2}} \cr & = 4.88 \times {10^3}Hz \cr & \simeq 5\,kHz \cr} $$
In solids, Velocity of wave $$V = \sqrt {\frac{Y}{\rho }} = \sqrt {\frac{{9.27 \times {{10}^{10}}}}{{2.7 \times {{10}^3}}}} $$
$$v = 5.85 \times {10^3}m/\sec $$
Since rod is clamped at middle fundamental wave shape is as follow

$$\eqalign{ & \frac{\lambda }{2} = L \cr & \Rightarrow \,\,\lambda = 2\,L \cr & \lambda = 1.2\,m\left( {\because \,\,L = 60\,cm = 0.6\,m\left( {{\text{given}}} \right)} \right) \cr & {\text{Using, }}v = f\lambda \cr & \Rightarrow \,\,f = \frac{v}{\lambda } = \frac{{5.85 \times {{10}^3}}}{{1.2}} \cr & = 4.88 \times {10^3}Hz \cr & \simeq 5\,kHz \cr} $$