Question
A glass prism of refractive index 1.5 is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if
A glass prism of refractive index 1.5 is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if

A.
$$\sin \theta \geqslant \frac{8}{9}$$
B.
$$\frac{2}{3} < \sin \theta < \frac{8}{9}$$
C.
$$\sin \theta \leqslant \frac{2}{3}$$
D.
None of these
Answer :
$$\sin \theta \geqslant \frac{8}{9}$$
Solution :
The phenomenon of total internal reflection takes place during reflection at $$P.$$
$$\sin \theta = \frac{1}{{_g^w\mu }}\,\,\,\,.....\left( {\text{i}} \right)$$
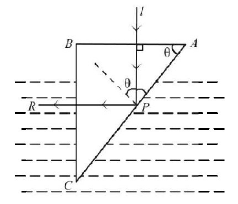
Now, $$_g^w\mu = \frac{{_g^a\mu }}{{_w^a\mu }}$$
$$\eqalign{ & = \frac{{1.5}}{{\frac{4}{3}}} \cr & = 1.125 \cr & \therefore \,\,\sin \theta = \frac{1}{{1.125}} \cr & = \frac{8}{9} \cr} $$
$$\therefore \,\,\sin \theta $$ should be greater than $$\frac{8}{9}.$$
The phenomenon of total internal reflection takes place during reflection at $$P.$$
$$\sin \theta = \frac{1}{{_g^w\mu }}\,\,\,\,.....\left( {\text{i}} \right)$$

Now, $$_g^w\mu = \frac{{_g^a\mu }}{{_w^a\mu }}$$
$$\eqalign{ & = \frac{{1.5}}{{\frac{4}{3}}} \cr & = 1.125 \cr & \therefore \,\,\sin \theta = \frac{1}{{1.125}} \cr & = \frac{8}{9} \cr} $$
$$\therefore \,\,\sin \theta $$ should be greater than $$\frac{8}{9}.$$
