Question
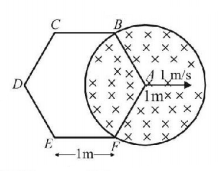
A cylindrical region of radius $$1\,m$$ has instantaneous homogenous magnetic field of $$5T$$ and it is increasing at a rate of $$2T/s.$$ A regular hexagonal loop $$ABCDEFA$$ of side $$1\,m$$ is being drawn in to the region with a constant speed of $$1\,m/s$$ as shown in the figure. What is the magnitude of emf developed in the loop just after the shown instant when the corner $$A$$ of the hexagon is coinciding with the centre of the circle ?
A cylindrical region of radius $$1\,m$$ has instantaneous homogenous magnetic field of $$5T$$ and it is increasing at a rate of $$2T/s.$$ A regular hexagonal loop $$ABCDEFA$$ of side $$1\,m$$ is being drawn in to the region with a constant speed of $$1\,m/s$$ as shown in the figure. What is the magnitude of emf developed in the loop just after the shown instant when the corner $$A$$ of the hexagon is coinciding with the centre of the circle ?
A.
$$\frac{5}{{\sqrt 3 }}V$$
B.
$$\frac{{2\pi }}{3}V$$
C.
$$\left( {5\sqrt 3 + \frac{{2\pi }}{3}} \right)V$$
D.
$$\left( {5\sqrt 3 + \pi } \right)V$$
Answer :
$$\left( {5\sqrt 3 + \frac{{2\pi }}{3}} \right)V$$
Solution :
The induced emf across the ends $$B$$ and $$F$$ due to motion of the loop,
$${e_1} = Bv\left( {BF} \right) = 5 \times 1 \times 2\sin {60^ \circ } = 5\sqrt 3 \,V.$$
The induced emf across the loop due to change in magnetic field
$$\eqalign{ & {e_2} = A\frac{{dB}}{{dt}} = \frac{{\pi {R^2}}}{3}\left( {\frac{{dB}}{{dt}}} \right) = \frac{{\pi {{\left( 1 \right)}^2}}}{3} \times 2 = \frac{{2\pi }}{3}V. \cr & {\text{So}}\,\,e = {e_1} + {e_2} = \left( {5\sqrt 3 + \frac{{2\pi }}{3}} \right)V. \cr} $$
The induced emf across the ends $$B$$ and $$F$$ due to motion of the loop,
$${e_1} = Bv\left( {BF} \right) = 5 \times 1 \times 2\sin {60^ \circ } = 5\sqrt 3 \,V.$$
The induced emf across the loop due to change in magnetic field
$$\eqalign{ & {e_2} = A\frac{{dB}}{{dt}} = \frac{{\pi {R^2}}}{3}\left( {\frac{{dB}}{{dt}}} \right) = \frac{{\pi {{\left( 1 \right)}^2}}}{3} \times 2 = \frac{{2\pi }}{3}V. \cr & {\text{So}}\,\,e = {e_1} + {e_2} = \left( {5\sqrt 3 + \frac{{2\pi }}{3}} \right)V. \cr} $$
