Question
A current $$I$$ flows in the anticlockwise direction through a square loop of side a lying in the $$XOY$$ plane with its center at the origin. The magnetic induction at the center of the square loop is
A.
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}{{\hat e}_x}$$
B.
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}{{\hat e}_z}$$
C.
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi {a^2}}}{{\hat e}_z}$$
D.
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi {a^2}}}{{\hat e}_x}$$
Answer :
$$\frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}{{\hat e}_z}$$
Solution :
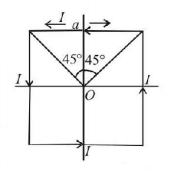
Field due to one side of loop at $$O = \frac{{{\mu _0}I}}{{4\pi \left( {\frac{a}{2}} \right)}}\left( {2\sin {{45}^ \circ }} \right)$$
Field at $$O$$ due to all four sides is along unit vector $${{\hat e}_z}$$
$$\therefore $$ Total field $$ = 4.\frac{{{\mu _0}I}}{{4\pi \left( {\frac{a}{2}} \right)}}\left( {2\sin {{45}^ \circ }} \right)$$
$$ = \frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}$$

Field due to one side of loop at $$O = \frac{{{\mu _0}I}}{{4\pi \left( {\frac{a}{2}} \right)}}\left( {2\sin {{45}^ \circ }} \right)$$
Field at $$O$$ due to all four sides is along unit vector $${{\hat e}_z}$$
$$\therefore $$ Total field $$ = 4.\frac{{{\mu _0}I}}{{4\pi \left( {\frac{a}{2}} \right)}}\left( {2\sin {{45}^ \circ }} \right)$$
$$ = \frac{{2\sqrt 2 {\mu _0}I}}{{\pi a}}$$