Question
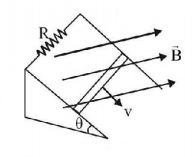
A conducting wire of mass $$m$$ slides down two smooth conducting bars, set at an angle $$\theta $$ to the horizintal as shown in Fig. The separation between the bars is $$l.$$ The system is located in the magnetic field $$B,$$ perpendicular to the plane of the sliding wire and bars. The constant velocity of the wire is
A conducting wire of mass $$m$$ slides down two smooth conducting bars, set at an angle $$\theta $$ to the horizintal as shown in Fig. The separation between the bars is $$l.$$ The system is located in the magnetic field $$B,$$ perpendicular to the plane of the sliding wire and bars. The constant velocity of the wire is
A.
$$\frac{{mgR\sin \theta }}{{{B^2}{l^2}}}$$
B.
$$\frac{{mgR\sin \theta }}{{B{l^3}}}$$
C.
$$\frac{{mgR\sin \theta }}{{{B^2}{l^5}}}$$
D.
$$\frac{{mgR\sin \theta }}{{B{l^4}}}$$
Answer :
$$\frac{{mgR\sin \theta }}{{{B^2}{l^2}}}$$
Solution :
Component of weight along the inclined plane $$ = mg\sin \theta $$
Again, $$F = BI\ell = B\frac{{B\ell v}}{R}\ell = \frac{{{B^2}{\ell ^2}v}}{R}$$
Now, $$\frac{{{B^2}{\ell ^2}v}}{R} = mg\sin \theta \,{\text{or}}\,v = \frac{{mgR\sin \theta }}{{{B^2}{l^2}}}$$
Component of weight along the inclined plane $$ = mg\sin \theta $$
Again, $$F = BI\ell = B\frac{{B\ell v}}{R}\ell = \frac{{{B^2}{\ell ^2}v}}{R}$$
Now, $$\frac{{{B^2}{\ell ^2}v}}{R} = mg\sin \theta \,{\text{or}}\,v = \frac{{mgR\sin \theta }}{{{B^2}{l^2}}}$$
