Question
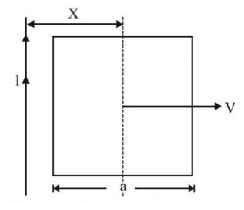
A conducting square frame of side $$'a'$$ and a long straight wire carrying current $$I$$ are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity $$'V'.$$ The emf induced in the frame will be proportional to
A conducting square frame of side $$'a'$$ and a long straight wire carrying current $$I$$ are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity $$'V'.$$ The emf induced in the frame will be proportional to
A.
$$\frac{1}{{{{\left( {2x - a} \right)}^2}}}$$
B.
$$\frac{1}{{{{\left( {2x + a} \right)}^2}}}$$
C.
$$\frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}}$$
D.
$$\frac{1}{{{x^2}}}$$
Answer :
$$\frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}}$$
Solution :
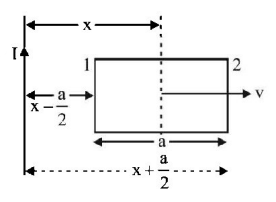
Emf induced in side 1 of frame $${e_1} = {B_1}V\ell $$
$${B_1} = \frac{{{\mu _0}I}}{{2\pi \left( {x - \frac{a}{2}} \right)}}$$
Emf induced in side 2 of frame $${e_2} = {B_2}V\ell $$
$${B_2} = \frac{{{\mu _0}I}}{{2\pi \left( {x + \frac{a}{2}} \right)}}$$
Emf induced in square frame
$$\eqalign{ & e = {B_1}V\ell - {B_2}V\ell \cr & = \frac{{{\mu _0}I}}{{2\pi \left( {x - \frac{a}{2}} \right)}}\ell v - \frac{{{\mu _0}I}}{{2\pi \left( {x + \frac{a}{2}} \right)}}\ell v \cr & {\text{or,}}\,\,e \propto \frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}} \cr} $$

Emf induced in side 1 of frame $${e_1} = {B_1}V\ell $$
$${B_1} = \frac{{{\mu _0}I}}{{2\pi \left( {x - \frac{a}{2}} \right)}}$$
Emf induced in side 2 of frame $${e_2} = {B_2}V\ell $$
$${B_2} = \frac{{{\mu _0}I}}{{2\pi \left( {x + \frac{a}{2}} \right)}}$$
Emf induced in square frame
$$\eqalign{ & e = {B_1}V\ell - {B_2}V\ell \cr & = \frac{{{\mu _0}I}}{{2\pi \left( {x - \frac{a}{2}} \right)}}\ell v - \frac{{{\mu _0}I}}{{2\pi \left( {x + \frac{a}{2}} \right)}}\ell v \cr & {\text{or,}}\,\,e \propto \frac{1}{{\left( {2x - a} \right)\left( {2x + a} \right)}} \cr} $$
