Question
A coil of wire having inductance and resistance has a conducting ring placed coaxially within it. The coil is connected to a battery at time $$t = 0,$$ so that a time-dependent current $${I_1}\left( t \right)$$ starts flowing through the coil. If $${I_2}\left( t \right)$$ is the current induced in the ring, and $$B\left( t \right)$$ is the magnetic field at the axis of the coil due to $${I_1}\left( t \right),$$ then as a function of time $$\left( {t > 0} \right)$$ the product $${I_2}\left( t \right)B\left( t \right)$$
A.
increases with time
B.
decreases with time
C.
does not vary with time
D.
passes through a maximum
Answer :
decreases with time
Solution :
KEY CONCEPT: The magnetic field at the centre of the coil
$$B\left( t \right) = {\mu _0}n{I_1}.$$
As the current increases, $$B$$ will also increase with time till it reaches a maximum value (when the current becomes steady).
The induced emf in the ring
$$e = - \frac{{d\phi }}{{dt}} = - \frac{d}{{dt}}\left( {\overrightarrow B .\overrightarrow A } \right) = - A\frac{d}{{dt}}\left( {{\mu _0}n{I_1}} \right)$$
∴ The induced current in the ring
$${I_2}\left( t \right) = \frac{{\left| e \right|}}{R} = \frac{{{\mu _0}nA}}{R}\frac{{d{I_1}}}{{dt}}$$
[NOTE : $$\frac{{d{I_1}}}{{dt}}$$ decreases with time and hence $${I_2}$$ also decreases with time.]
Where $${I_1} = {I_{\max }}\left( {1 - {e^{ - \frac{t}{\tau }}}} \right)$$
The relevant graphs are
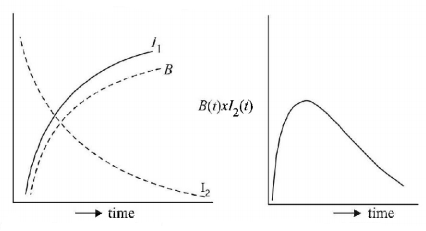
KEY CONCEPT: The magnetic field at the centre of the coil
$$B\left( t \right) = {\mu _0}n{I_1}.$$
As the current increases, $$B$$ will also increase with time till it reaches a maximum value (when the current becomes steady).
The induced emf in the ring
$$e = - \frac{{d\phi }}{{dt}} = - \frac{d}{{dt}}\left( {\overrightarrow B .\overrightarrow A } \right) = - A\frac{d}{{dt}}\left( {{\mu _0}n{I_1}} \right)$$
∴ The induced current in the ring
$${I_2}\left( t \right) = \frac{{\left| e \right|}}{R} = \frac{{{\mu _0}nA}}{R}\frac{{d{I_1}}}{{dt}}$$
[NOTE : $$\frac{{d{I_1}}}{{dt}}$$ decreases with time and hence $${I_2}$$ also decreases with time.]
Where $${I_1} = {I_{\max }}\left( {1 - {e^{ - \frac{t}{\tau }}}} \right)$$
The relevant graphs are

