Question
A charged particle of specific charge $$\left( {\frac{{{\text{charge}}}}{{{\text{mass}}}}} \right)\alpha $$ is released from origin at time $$t = 0$$ with velocity $$\vec v = {v_0}\left( {\hat i + \hat j} \right)$$ in uniform magnetic field $$\vec B = {B_0}\hat i.$$ Coordinates of the particle at time $$t = \frac{\pi }{{\left( {{B_0}\alpha } \right)}}$$ are
A.
$$\left( {\frac{{{v_0}}}{{2{B_0}\alpha }},\frac{{\sqrt 2 {v_0}}}{{\alpha {B_0}}},\frac{{ - {v_0}}}{{{B_0}\alpha }}} \right)$$
B.
$$\left( {\frac{{ - {v_0}}}{{2{B_0}\alpha }},0,0} \right)$$
C.
$$\left( {0,\frac{{2{v_0}}}{{{B_0}\alpha }},\frac{{{v_0}\pi }}{{2{B_0}\alpha }}} \right)$$
D.
$$\left( {\frac{{{v_0}\pi }}{{{B_0}\alpha }},0,\frac{{ - 2{v_0}}}{{{B_0}\alpha }}} \right)$$
Answer :
$$\left( {\frac{{{v_0}\pi }}{{{B_0}\alpha }},0,\frac{{ - 2{v_0}}}{{{B_0}\alpha }}} \right)$$
Solution :
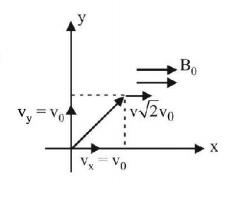
$$\alpha = \frac{q}{m},$$ path of the particle will be a helix of time period,
$$T = \frac{{2\pi m}}{{{B_0}q}} = \frac{{2\pi }}{{{B_0}\alpha }}$$
The give time $$t = \frac{\pi }{{{B_0}\alpha }} = \frac{T}{2}$$
∴ Coordinates of particle at time $$t = \frac{T}{2}$$ would be $$\left( {vx\frac{T}{2},0, - 2r} \right)$$
Here, $$r = \frac{{m{v_0}}}{{{B_0}q}} = \frac{{{v_0}}}{{{B_0}\alpha }}$$
∴ The coordinate are $$\left( {\frac{{{v_0}\pi }}{{{B_0}\alpha }},0,\frac{{ - 2{v_0}}}{{{B_0}\alpha }}} \right)$$

$$\alpha = \frac{q}{m},$$ path of the particle will be a helix of time period,
$$T = \frac{{2\pi m}}{{{B_0}q}} = \frac{{2\pi }}{{{B_0}\alpha }}$$
The give time $$t = \frac{\pi }{{{B_0}\alpha }} = \frac{T}{2}$$
∴ Coordinates of particle at time $$t = \frac{T}{2}$$ would be $$\left( {vx\frac{T}{2},0, - 2r} \right)$$
Here, $$r = \frac{{m{v_0}}}{{{B_0}q}} = \frac{{{v_0}}}{{{B_0}\alpha }}$$
∴ The coordinate are $$\left( {\frac{{{v_0}\pi }}{{{B_0}\alpha }},0,\frac{{ - 2{v_0}}}{{{B_0}\alpha }}} \right)$$