Question
A car, starting from rest, accelerates at the rate $$f$$ through a distance $$S,$$ then continues at constant speed for time $$t$$ and then decelerates at the rate $$\frac{f}{2}$$ to come to rest. If the total distance traversed is $$15 \,S ,$$ then-
A.
$$S = \frac{1}{6}f{t^2}$$
B.
$$S = ft$$
C.
$$S = \frac{1}{4}f{t^2}$$
D.
$$S = \frac{1}{{72}}f{t^2}$$
Answer :
$$S = \frac{1}{{72}}f{t^2}$$
Solution :
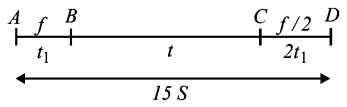
distance from $$A$$ to $$B$$ $$ = S = \frac{1}{2}ft_1^2 \Rightarrow ft_1^2 = 2S$$
Distance from $$B$$ to $$C$$ $$ = \left( {f{t_1}} \right)t$$
distance from $$C$$ to $$D$$ $$ = \frac{{{u^2}}}{{2a}} = \frac{{{{\left( {f{t_1}} \right)}^2}}}{{2\left( {\frac{f}{2}} \right)}} = ft_1^2 = 2S$$
$$\eqalign{ & \Rightarrow S + f\,{t_1}t + 2\,S = 15\,S \cr & \Rightarrow f\,{t_1}t = 12\,S \cr & {\text{But}}\,\frac{1}{2}f\,t_1^2 = S \cr} $$
On dividing the above two equations, we get $${t_1} = \frac{t}{6}$$
$$ \Rightarrow S = \frac{1}{2}f{\left( {\frac{t}{6}} \right)^2} = \frac{{f\,{t^2}}}{{72}} = \frac{1}{{72}}f\,{t^2}$$
distance from $$A$$ to $$B$$ $$ = S = \frac{1}{2}ft_1^2 \Rightarrow ft_1^2 = 2S$$
Distance from $$B$$ to $$C$$ $$ = \left( {f{t_1}} \right)t$$
distance from $$C$$ to $$D$$ $$ = \frac{{{u^2}}}{{2a}} = \frac{{{{\left( {f{t_1}} \right)}^2}}}{{2\left( {\frac{f}{2}} \right)}} = ft_1^2 = 2S$$

$$\eqalign{ & \Rightarrow S + f\,{t_1}t + 2\,S = 15\,S \cr & \Rightarrow f\,{t_1}t = 12\,S \cr & {\text{But}}\,\frac{1}{2}f\,t_1^2 = S \cr} $$
On dividing the above two equations, we get $${t_1} = \frac{t}{6}$$
$$ \Rightarrow S = \frac{1}{2}f{\left( {\frac{t}{6}} \right)^2} = \frac{{f\,{t^2}}}{{72}} = \frac{1}{{72}}f\,{t^2}$$




