Question
A car is moving along a straight road with a uniform acceleration. It passes through two points $$P$$ and $$Q$$ separated by a distance with velocity $$30\,km/h$$ and $$40\,km/h$$ respectively. The velocity of the car midway between $$P$$ and $$Q$$ is
A.
$$33.3\,km/h$$
B.
$$20\sqrt 2 \,km/h$$
C.
$$25\sqrt 2 \,km/h$$
D.
$$0.35\,km/h$$
Answer :
$$25\sqrt 2 \,km/h$$
Solution :
Let $$x$$ be the total distance between points $$P$$ and $$Q$$ and $$v$$ be the velocity of car while passing a certain middle point of $$PQ.$$ If $$a$$ is the acceleration of the car, then
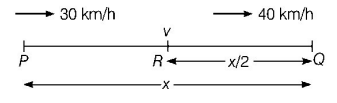
For part $$PQ,$$
$$\eqalign{ & {40^2} - {30^2} = 2ax \cr & {\text{or}}\,a = \frac{{350}}{x}\,......\left( {\text{i}} \right) \cr} $$
For part $$RQ,$$
$${40^2} - {v^2} = \frac{{2ax}}{2}\,......\left( {{\text{ii}}} \right)$$
Putting value of a from Eq. (i) in Eq. (ii), we have
$$\eqalign{ & {40^2} - {v^2} = 2\left( {\frac{{350}}{x}} \right)\frac{x}{2} \cr & {\text{or}}\,\,{40^2} - {v^2} = 350\quad \cr & {\text{or}}\,\,{v^2} = 1250 \cr & \Rightarrow v = 25\sqrt 2 \,km/h \cr} $$
Let $$x$$ be the total distance between points $$P$$ and $$Q$$ and $$v$$ be the velocity of car while passing a certain middle point of $$PQ.$$ If $$a$$ is the acceleration of the car, then

For part $$PQ,$$
$$\eqalign{ & {40^2} - {30^2} = 2ax \cr & {\text{or}}\,a = \frac{{350}}{x}\,......\left( {\text{i}} \right) \cr} $$
For part $$RQ,$$
$${40^2} - {v^2} = \frac{{2ax}}{2}\,......\left( {{\text{ii}}} \right)$$
Putting value of a from Eq. (i) in Eq. (ii), we have
$$\eqalign{ & {40^2} - {v^2} = 2\left( {\frac{{350}}{x}} \right)\frac{x}{2} \cr & {\text{or}}\,\,{40^2} - {v^2} = 350\quad \cr & {\text{or}}\,\,{v^2} = 1250 \cr & \Rightarrow v = 25\sqrt 2 \,km/h \cr} $$




