Question
A car accelerates from rest at a constant rate $$\alpha $$ for some time, after which it decelerates at a constant rate $$\beta $$ and comes to rest. If the total time elapsed is $$t,$$ then the maximum velocity acquired by the car is
A.
$$\left( {\frac{{{\alpha ^2} + {\beta ^2}}}{{\alpha \beta }}} \right)t$$
B.
$$\left( {\frac{{{\alpha ^2} - {\beta ^2}}}{{\alpha \beta }}} \right)$$
C.
$$\frac{{\left( {\alpha + \beta } \right)t}}{{\alpha \beta }}$$
D.
$$\frac{{\alpha \beta t}}{{\alpha + \beta }}$$
Answer :
$$\frac{{\alpha \beta t}}{{\alpha + \beta }}$$
Solution :
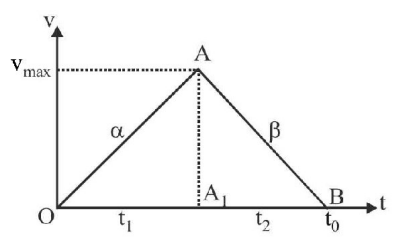
$$\eqalign{ & {\text{In}}\,{\text{fig}}{\text{.,}}\,A{A_1} = {v_{\max .}} = \alpha {t_1} = \beta {t_2} \cr & {\text{But}}\,t = {t_1} + {t_2} = \frac{{{v_{\max }}}}{\alpha } + \frac{{{v_{\max }}}}{\beta } \cr & = {v_{\max }}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right) = {v_{\max }}\left( {\frac{{\alpha + \beta }}{{\alpha \beta }}} \right) \cr & {\text{or,}}\,\,{v_{\max }} = t\left( {\frac{{\alpha \beta }}{{\alpha + \beta }}} \right) \cr} $$

$$\eqalign{ & {\text{In}}\,{\text{fig}}{\text{.,}}\,A{A_1} = {v_{\max .}} = \alpha {t_1} = \beta {t_2} \cr & {\text{But}}\,t = {t_1} + {t_2} = \frac{{{v_{\max }}}}{\alpha } + \frac{{{v_{\max }}}}{\beta } \cr & = {v_{\max }}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right) = {v_{\max }}\left( {\frac{{\alpha + \beta }}{{\alpha \beta }}} \right) \cr & {\text{or,}}\,\,{v_{\max }} = t\left( {\frac{{\alpha \beta }}{{\alpha + \beta }}} \right) \cr} $$




