Question
A car accelerates from rest at a constant rate $$\alpha $$ for some time, after which it decelerates at a constant rate $$\beta $$ and comes to rest. If the total time elapsed is $$t,$$ then the maximum velocity acquired by the car is
A.
$$\left( {\frac{{{\alpha ^2} + {\beta ^2}}}{{\alpha \beta }}} \right)t$$
B.
$$\left( {\frac{{{\alpha ^2} - {\beta ^2}}}{{\alpha \beta }}} \right)t$$
C.
$$\frac{{\left( {\alpha + \beta } \right)t}}{{\alpha \beta }}$$
D.
$$\left( {\frac{{\alpha \beta t}}{{\alpha + \beta }}} \right)$$
Answer :
$$\left( {\frac{{\alpha \beta t}}{{\alpha + \beta }}} \right)$$
Solution :
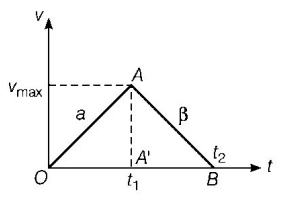
This situation is plotted on $$\left( {v - t} \right)$$ graph. In $$\left( {v - t} \right)$$ graph, $$OA$$ represents the accelerated part and $$AB$$ represents the decelerated part.
Let $${t_1}$$ and $${t_2}$$ be the times for part $$OA$$ and $$AB$$ respectively.
At point $$A$$ velocity is maximum and let it be $${v_{\max }}.$$
$$\eqalign{ & \therefore {v_{\max }} = \alpha {t_1} = \beta {t_2} \cr & {\text{But}}\,\,t = {t_1} + {t_2} = \frac{{{v_{\max }}}}{\alpha } + \frac{{{v_{\max }}}}{\beta } \cr & = {v_{\max }}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right) \cr & = {v_{\max }}\left( {\frac{{\alpha + \beta }}{{\alpha \beta }}} \right) \cr & {\text{or}}\,\,{v_{\max }} = t\left( {\frac{{\alpha \beta }}{{\alpha + \beta }}} \right) \cr} $$
Alternative
This problem can also be solved by checking the dimensions on both sides. On checking the dimensions we note that the dimensions of option (D) match with that of velocity.

This situation is plotted on $$\left( {v - t} \right)$$ graph. In $$\left( {v - t} \right)$$ graph, $$OA$$ represents the accelerated part and $$AB$$ represents the decelerated part.
Let $${t_1}$$ and $${t_2}$$ be the times for part $$OA$$ and $$AB$$ respectively.
At point $$A$$ velocity is maximum and let it be $${v_{\max }}.$$
$$\eqalign{ & \therefore {v_{\max }} = \alpha {t_1} = \beta {t_2} \cr & {\text{But}}\,\,t = {t_1} + {t_2} = \frac{{{v_{\max }}}}{\alpha } + \frac{{{v_{\max }}}}{\beta } \cr & = {v_{\max }}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right) \cr & = {v_{\max }}\left( {\frac{{\alpha + \beta }}{{\alpha \beta }}} \right) \cr & {\text{or}}\,\,{v_{\max }} = t\left( {\frac{{\alpha \beta }}{{\alpha + \beta }}} \right) \cr} $$
Alternative
This problem can also be solved by checking the dimensions on both sides. On checking the dimensions we note that the dimensions of option (D) match with that of velocity.




