Question
A body of mass $$\left( {4m} \right)$$ is lying in $$xy$$ -plane at rest. It suddenly explodes into three pieces. Two pieces each of mass $$\left( {m} \right)$$ move perpendicular to each other with equal speeds $$\left( {v} \right).$$ The total kinetic energy generated due to explosion is
A.
$$m{v^2}$$
B.
$$\frac{3}{2}m{v^2}$$
C.
$$2m{v^2}$$
D.
$$4m{v^2}$$
Answer :
$$\frac{3}{2}m{v^2}$$
Solution :
Conserve the momentum of third mass with the resultant momentum of 1st and 2nd masses. After getting velocity of third mass, calculate total kinetic energy.
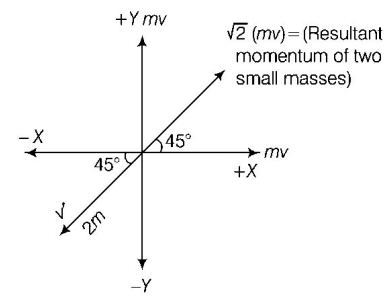
According to question, the third part of mass $$2m$$ will move as shown in the figure, because the total momentum of the system after explosion must remain zero. Let the velocity of third part be $$v'.$$
From the conservation of momentum $$\sqrt 2 \left( {mv} \right) = \left( {2m} \right) \times v' \Rightarrow v' = \frac{v}{{\sqrt 2 }}$$
So, total kinetic energy generated by the explosion
$$\eqalign{ & = \frac{1}{2}m{v^2} + \frac{1}{2}m{v^2} + \frac{1}{2}\left( {2m} \right){{v'}^2} \cr & = m{v^2} + m \times {\left( {\frac{v}{{\sqrt 2 }}} \right)^2} = m{v^2} + \frac{{m{v^2}}}{2} = \frac{3}{2}m{v^2} \cr} $$
Conserve the momentum of third mass with the resultant momentum of 1st and 2nd masses. After getting velocity of third mass, calculate total kinetic energy.

According to question, the third part of mass $$2m$$ will move as shown in the figure, because the total momentum of the system after explosion must remain zero. Let the velocity of third part be $$v'.$$
From the conservation of momentum $$\sqrt 2 \left( {mv} \right) = \left( {2m} \right) \times v' \Rightarrow v' = \frac{v}{{\sqrt 2 }}$$
So, total kinetic energy generated by the explosion
$$\eqalign{ & = \frac{1}{2}m{v^2} + \frac{1}{2}m{v^2} + \frac{1}{2}\left( {2m} \right){{v'}^2} \cr & = m{v^2} + m \times {\left( {\frac{v}{{\sqrt 2 }}} \right)^2} = m{v^2} + \frac{{m{v^2}}}{2} = \frac{3}{2}m{v^2} \cr} $$