Question
A body is at rest at $$x =0.$$ At $$t=0,$$ it starts moving in the positive x-direction with a constant acceleration. At the same instant another body passes through $$x = 0$$ moving in the positive x-direction with a constant speed. The position of the first body is given by $${x_1}\left( t \right)$$ after time $$'t\, ’;$$ and that of the second body by $${x_2}\left( t \right)$$ after the same time interval. Which of the following graphs correctly describes $$\left( {{x_1} - {x_2}} \right)$$ as a function of time $$'t \,'$$ ?
A.


B.


C.


D.


Answer :


Solution :
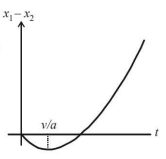
For the body starting from rest
$${x_1} = 0 + \frac{1}{2}a{t^2} \Rightarrow {x_1} = \frac{1}{2}a{t^2}$$
For the body moving with constant speed
$$\eqalign{ & {x_2} = vt \cr & \therefore {x_1} - {x_2} = \frac{1}{2}a{t^2} - vt \cr & \Rightarrow \frac{{d\left( {{x_1} - {x_2}} \right)}}{{dt}} = at - v \cr & {\text{at }}t = 0,\,\,\,\,\,\,{x_1} - {x_2} = 0 \cr & {\text{For }}t < \frac{v}{a};\,{\text{the slope is negative}} \cr & {\text{For }}t = \frac{v}{a};\,{\text{the slope is zero}} \cr & {\text{For }}t > \frac{v}{a};\,{\text{the slope is positive}} \cr} $$
These characteristics are represented by graph (B).

For the body starting from rest
$${x_1} = 0 + \frac{1}{2}a{t^2} \Rightarrow {x_1} = \frac{1}{2}a{t^2}$$
For the body moving with constant speed
$$\eqalign{ & {x_2} = vt \cr & \therefore {x_1} - {x_2} = \frac{1}{2}a{t^2} - vt \cr & \Rightarrow \frac{{d\left( {{x_1} - {x_2}} \right)}}{{dt}} = at - v \cr & {\text{at }}t = 0,\,\,\,\,\,\,{x_1} - {x_2} = 0 \cr & {\text{For }}t < \frac{v}{a};\,{\text{the slope is negative}} \cr & {\text{For }}t = \frac{v}{a};\,{\text{the slope is zero}} \cr & {\text{For }}t > \frac{v}{a};\,{\text{the slope is positive}} \cr} $$
These characteristics are represented by graph (B).




