Question
A boat is sent across a river with a velocity of $$8\,km\,{h^{ - 1}}.$$ If the resultant velocity of boat is $$10\,km\,{h^{ - 1}},$$ then velocity of river is
A.
$$12.8\,km\,{h^{ - 1}}$$
B.
$$6\,km\,{h^{ - 1}}$$
C.
$$8\,km\,{h^{ - 1}}$$
D.
$$10\,km\,{h^{ - 1}}$$
Answer :
$$6\,km\,{h^{ - 1}}$$
Solution :
The situation is depicted in figure.
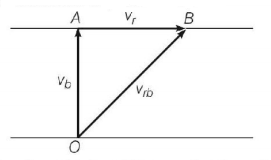
Let $${v_b}$$ be the velocity of boat, $${v_r}$$ be the velocity of river and $${v_{rb}}$$ be the resultant velocity of boat.
From figure and concept of relative velocity
$$\eqalign{ & v_{rb}^2 = v_r^2 + v_b^2 \cr & \therefore {v_r} = \sqrt {v_{rb}^2 - v_b^2} = \sqrt {{{10}^2} - {8^2}} = 6\,km\,{h^{ - 1}} \cr} $$
The situation is depicted in figure.

Let $${v_b}$$ be the velocity of boat, $${v_r}$$ be the velocity of river and $${v_{rb}}$$ be the resultant velocity of boat.
From figure and concept of relative velocity
$$\eqalign{ & v_{rb}^2 = v_r^2 + v_b^2 \cr & \therefore {v_r} = \sqrt {v_{rb}^2 - v_b^2} = \sqrt {{{10}^2} - {8^2}} = 6\,km\,{h^{ - 1}} \cr} $$




