Question
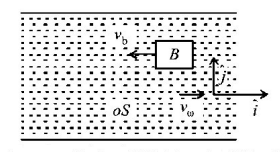
A boat $$B$$ is moving upstream with velocity $$3\,m/s$$ with respect to ground. An observer standing on boat observes that a swimmer $$S$$ is crossing the river perpendicular to the direction of motion of boat. If river flow velocity is $$4\,m/s$$ and swimmer crosses the river of width $$100\,m$$ in $$50\,\sec,$$ then
A boat $$B$$ is moving upstream with velocity $$3\,m/s$$ with respect to ground. An observer standing on boat observes that a swimmer $$S$$ is crossing the river perpendicular to the direction of motion of boat. If river flow velocity is $$4\,m/s$$ and swimmer crosses the river of width $$100\,m$$ in $$50\,\sec,$$ then
A.
velocity of swimmer w.r.t ground is $$\sqrt {13} \,m/s$$
B.
drift of swimmer along river is zero
C.
drift of swimmer along river will be $$50\,m$$
D.
velocity of swimmer w.r.t ground is $$2\,m/s$$
Answer :
velocity of swimmer w.r.t ground is $$\sqrt {13} \,m/s$$
Solution :
$$\eqalign{ & {\overrightarrow v _{SB}} = v\hat j = {\overrightarrow v _s} + 3\hat i \cr & {\overrightarrow v _S} = v\hat j - 3\hat i\,{\text{and}}\,v = \frac{{100}}{{50}} = 2\,m/s \cr & \therefore \left| {{{\overrightarrow v }_S}} \right| = \sqrt {{v^2} + {{\left( 3 \right)}^2}} = \sqrt {{2^2} + 9} = \sqrt {13} \,m/s \cr & {\text{Drift}} = 50 \times 3 = 150\,m \cr} $$
$$\eqalign{ & {\overrightarrow v _{SB}} = v\hat j = {\overrightarrow v _s} + 3\hat i \cr & {\overrightarrow v _S} = v\hat j - 3\hat i\,{\text{and}}\,v = \frac{{100}}{{50}} = 2\,m/s \cr & \therefore \left| {{{\overrightarrow v }_S}} \right| = \sqrt {{v^2} + {{\left( 3 \right)}^2}} = \sqrt {{2^2} + 9} = \sqrt {13} \,m/s \cr & {\text{Drift}} = 50 \times 3 = 150\,m \cr} $$




